Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.5 - Ex. 94

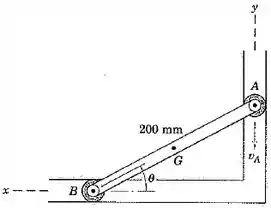
5/94) A barra com restrições do Prob.5/81 é reapresentada aqui . A extremidade A da barra possui uma velocidade descendente v A de 2 m / s durante um intervalo de seu movimento . Para a posição onde θ = 30 ° , determine pelo método dessa seção a velocidade angular ω de A B e a velocidade v G do ponto central G da barra .

Passo 1

Então galera , para acharmos a velocidade angular , devemos lembrar da relação :

v A = A C - ω

Sendo assim , precisamos primeiramente achar o módulo de A C - . O centro instantâneo de velocidade se encontra no ponto de interseção entre as retas perpendiculares às velocidades dos pontos da barra , logo , para θ = 30 ° , temos que :

A C - = 0,2 cos ⁡ 30 ° = 0,1732   m

Passo 2

Bom pessoal , utilizando as relações que achamos no passo anterior , obtemos que :

ω = v A A C - = 2 0,1732 = 11,55   r a d / s   S H

Agora podemos achar o módulo da velocidade do ponto central G da barra através da equação:

v G = C G - ω

Bom , analisando a trigonometria do sistema , obtemos que :

G = 0,1 * cos ⁡ 30 ° ; 0,1 sen ⁡ 30 °   e   C 0   ; 0,2 sen ⁡ 30 °

G = 0,0866   ; 0,05   e   C = (   0   ; 0,1 )

Logo ,

C G - = 0 - 0,0866 2 + 0,1 - 0,05 2 = 0,1

Sendo assim , temos que :

v G = 0,1 11,55 = 1,155   m / s

Resposta

ω = 11,55   r a d / s   S H

v G = 0,1 11,55 = 1,155   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o período de pequenas oscilações de uma pequena partícula que se move sem atrito dentro de uma superfície cilíndrica de raio R.
A haste ABC de massa total em é dobrada como mostrado e é apoiada em um plano vertical por um pino em B e uma mola de k constante em C. Se a extremidade C receber um pequeno deslocamento e for liberad
Uma biela é sustentada por um fio de faca no Ponto A; o período de suas pequenas oscilações é observado em 1,03 s. Sabendo que a distância r é de 150 mm, determine o raio centroidal de giração da biel
Uma esfera A de 14 onças e uma esfera C de 10 onças são fixadas às extremidades de uma haste AC de peso desprezível que pode girar em um plano vertical em torno de um eixo em B. Determine o período de
A borda interna de um volante de 85 libras é colocada em um fio de navalha e o período de suas pequenas oscilações é de 1,26 s. Determine o momento de inércia centróide do volante.