Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.5 - Ex. 101

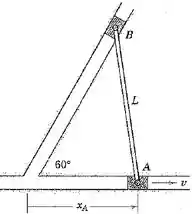
5/101) O mecanismo do Prob.5/27 é reapresentado aqui. No instante em que x A = 0,85 L , a velocidade do cursor em A é v = 2 m / s para a direita . Determine a velocidade correspondente do cursor B e a velocidade angular ω da barra A B se L = 0,8   m .

Passo 1

Então galera , a primeira coisa que devemos fazer é construir geométricamente a situação do problema . Sabemos que :

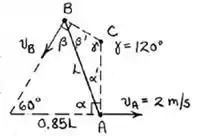
Aplicando a lei dos senos em relação ao triângulo indicado na figura, obtemos que :

sen ⁡ 60 ° L = sen ⁡ β 0,85   L  

Logo ,

β = 47,4 °

Sendo assim ,

α = 180 ° - 60 ° - 47,4 ° = 72,6 °

Passo 2

Continuando a análise da figura indicada no passo anterior , achamos que :

β + β ' = 90 °     →     β ' = 42,6

α + α ' = 90 °     →   α ' = 17,4 °

Sendo assim , aplicando aplicando a lei dos senos ao triângulo menor , obtemos que :

sen ⁡ γ L = sen ⁡ β ' A C -  

Logo ,

A C - = 0,782   L

Utilizando raciocínio análogo ao procedimento anterior , achamos que :

sen ⁡ γ L = sen ⁡ α ' B C -  

Portanto ,

  B C - = 0,345   L

Passo 3

Bom pessoal , aplicando as relações aprendidas neste capítulo , obtemos que :

v A = A C - ω    

Logo ,

  ω = v A A C - = 2 0,782 L = 2 0,782 0,8 = 3,2   r a d / s

Sendo assim , para acharmos a velocidade do cursor B basta aplicarmos a relação :

v B = B C - ω = 0,345 0,8 3,2 = 0,884   m / s

Resposta

ω = 3,2   r a d / s

v B = 0,884   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quando um corpo submerso se move em um fluido, as partículas deste fluido circulam em torno do corpo e adquirem energia cinética. No caso de uma esfera movendo-se em um fluido ideal, a energia cinétic
duas hastes uniformes AB e CD, cada uma com comprimento l e massa m, são fixadas às engrenagens conforme mostrado. Sabendo que a massa da engrenagem C está dentro e que a massa da engrenagem A é de 4m
Quatro barras de mesma massa m e comprimento igual a l são conectadas por pinos em A, B, C e D e podem se mover em um plano horizontal. As barras são fixadas a quatro molas de mesma constante k e estã
Três hastes idênticas são conectadas conforme mostrado. Se b = 3 4 l , determine a frequência de pequenas oscilações do sistema.
Uma placa fina de comprimento l repousa sobre um semicilindro deraio r. Deduza uma expressão para o período de pequenas oscilaçõesda p.