Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 94

16.94. A roda está rigidamente fixada à engrenagem A , que está engrenada às cremalheiras D e E . Se D tem uma velocidade V D = 1,8   m / s para a direita e a roda rola sobre o trilho C

sem deslizar, determine a velocidade da cremalheira E .

Passo 1

Movimento geral do plano: Como a roda rola sem escorregar na pista C, o IC (ponto de contato) está localizado no ponto de contato entre a roda e a pista C . Fig. a

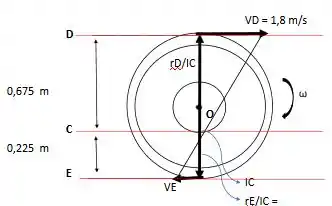
Fig. a

Passo 2

Através dos dados e da figura obtida, podemos obter os valores (comprimento) dos segmentos de linha r D e r E com relação ao nosso ponto de contato I C .

r D   I C =   0,675 m

r E   I C = 0,225   m

Passo 3

assim, a velocidade angular da engrenagem pode ser determinada de forma que relacione a velocidade no ponto D e seu segmento de linha r D / I C .

ω = V D r D I C = 1,8 0,675

ω = 2,667   r a d / s

Passo 4

Sabendo da velocidade angular da engrenagem, podemos então definir o valor da velocidade linear no ponto . ponto que coincide entre o ponto de contato, e os dentes da engrenagem com a cremalheira que é onde se origina a pista E .

V E = ω . r E I C

V E = 2,667   .   ( 0,225 )  

V E = 0,6   m / s

Resposta

V E =   0,6   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o período de pequenas oscilações de uma pequena partícula que se move sem atrito dentro de uma superfície cilíndrica de raio R.
A haste ABC de massa total em é dobrada como mostrado e é apoiada em um plano vertical por um pino em B e uma mola de k constante em C. Se a extremidade C receber um pequeno deslocamento e for liberad
Uma biela é sustentada por um fio de faca no Ponto A; o período de suas pequenas oscilações é observado em 1,03 s. Sabendo que a distância r é de 150 mm, determine o raio centroidal de giração da biel
Uma esfera A de 14 onças e uma esfera C de 10 onças são fixadas às extremidades de uma haste AC de peso desprezível que pode girar em um plano vertical em torno de um eixo em B. Determine o período de
A borda interna de um volante de 85 libras é colocada em um fio de navalha e o período de suas pequenas oscilações é de 1,26 s. Determine o momento de inércia centróide do volante.