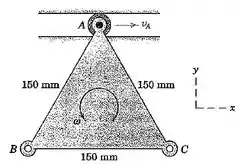
5/61) O vértice da placa em formato de triângulo eqüilátero possui uma velocidade para a direita , e a velocidade angular no sentido anti-horário da placa é . Determine a velocidade do vértice para o instante mostrado .
Passo 1
Então galera , a primeira coisa que devemos fazer é calcular o módulo da distância , onde M é o ponto médio da base BC, através da relação :
Além disso , pelas relações aprendidas nesta seção , sabemos que :
Sendo assim , temos que :
Substituindo pelos valores que já conhecemos , achamos que :