Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 69

5/69) O ciclista mostrado pedala regularmente para manter uma velocidade constante de 16   k m / h em oposição a uma leve brisa frontal . Calcule os módulos máximo e mínimo da velocidade absoluta do pedal A .

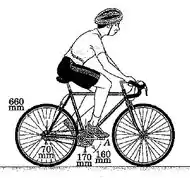
Passo 1

Falaaaaaaa meus amores, ceis tão bonzinho??

Bora resolver mais uma??

Então encostaaaa

Vamos considerar a direção das velocidades dos pedais (Observe o nosso D.C.L ).

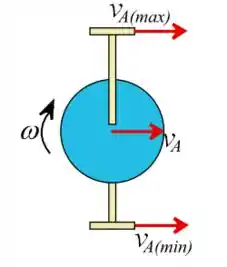
Passo 2

Agora iremos converter a velocidade da bicicleta de km/h para m/s

v o = 16   k m / h   × 1000   m 1   k m × 1 h 3600   s

= 4.44   m / s

Agora iremos calcualr a avelocidade angular do pedal

ω = d s d g × v o r w

Onde

d s é o diâmetro da roda dentada

d g é o diâmetro da engrenagem

r w é o raio da roda

Vamos substituir os valores numéricos

ω = 0.07 0.17 × 4 . 4 4 0.33

ω = 5.54   r a d / s

Passo 3

Bom iremos agora calcular o módulo da velocidade absoluta máxima

v A m á x = v o + v A / o

= v o + r p ω

Onde,

r p é a distância do pedal ao centro

Substituindo os valores numéricos

v A m á x = 4.44 + 0.16 × 5.54

v A m á x = 4.44 + 0.886

v A m á x = 5.326   m / s

Portanto, a magnitude da velocidade absoluta máxima é de 5.326   m / s .

Passo 4

Bom iremos agora calcular o módulo da velocidade absoluta mínima

v A m i n = v o - v A / o

= v o - r p ω

Onde,

r p é a distância do pedal ao centro

Substituindo os valores numéricos

v A m i n = 4.44 - 0.16 × 5.54

v A m i n = 4.44 + 0.886

v A m i n = 3.554     m / s

Portanto, a magnitude da velocidade absoluta mínima é de 3.554   m / s .

Resposta

Portanto, a magnitude da velocidade absoluta máxima é de 5.326   m / s .

Portanto, a magnitude da velocidade absoluta mínima é de 3.554   m / s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5/114) O cilindro pequeno rola sobre asuperfície do cilindro grande sem deslizar . Utilizando o centro instantâneo de velocidade nula do cilindro pequeno , determine a velocidade v A do ponto A indica
5/111) Os elementos do mecanismo para a implantação da lança do magnetômetro de uma nave espacial são reapresentados aqui a partir do Prob.5/87 . Pelo método dessa seção , determine a velocidade angul
5/116) A engrenagem D (os dentes não são mostrados) gira no sentido horário em torno de O com uma velocidade angular constante de 4r a d / s . O setor de 90 °A O B está montado sobre um eixo independe
5/117) O projeto do mecanismo mostrado , o cursor A deve deslizar ao longo do eixo fixo conform o ângulo θ aumenta . Quando θ = 30 ° , o elemento de controle em D deve ter uma componente de velocidade
5/119) O movimento do rolete A contra sua mola restritiva é controlado pelo movimento descendente do êmbolo E . Para um intervalo de movimento a velocidade de E é v = 0,2m / s . Determine a velocidade