Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 5.Problemas - Ex. 182

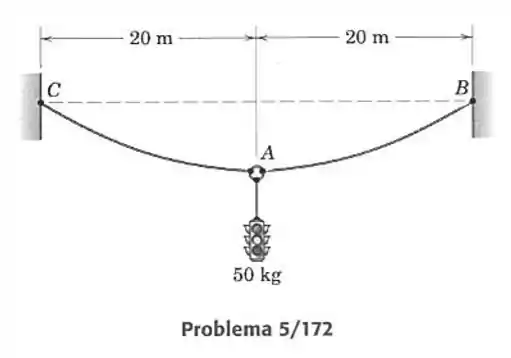
172- Um sinal de trânsito está suspenso por dois cabos de 21   m de comprimento, que têm uma massa de 1.2   k g por metro. Determine a deflexão vertical δ do anel de junção A relativamente a sua posição antes do sinal ser colocado.

Passo 1

O peso específico μ da corda é:

μ = 1.2 k g m × 9.81 = 11.772 N m

E o comprimento da corda C A e da corda A B vale 21   m .

Fazendo o diagrama de forças em A temos:

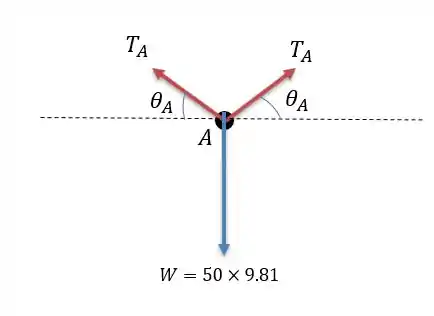
Onde consideramos um θ A formada nesse ponto (isso é, o ponto A não é origem de nenhuma equação de catenária) e uma tração A igual dos dois lados, fazendo a somatória das forças verticais temos:

2 T A sin ⁡ θ A = W

T A sin ⁡ θ A = W 2  

Onde vamos considerar apenas como W pois vamos analisar a deflexão dele mais tarde com W igual ao peso do sinal que é de 490.5   N e com W igual a zero. Pois a diferença entre as duas posições será o valor de δ . Ou a diferença relativa.

Passo 2

A equação de T A pode ser escrita como:

T A = T 0 + μ y A

E θ pode ser:

t g   θ = s i n h μ x T 0

θ A = t g - 1   ( sinh ⁡ μ x A T 0

Logo a equação será:

T 0 + μ y A t g - 1 sinh ⁡ μ x A T 0 = W 2 ( 1 )

Passo 3

Agora temos que pegar dois pontos de alguma catenária e colocar na equação, vamos pegar os pontos A   e B , em relação a A sabemos que B vale ( x a + 20 , y a + h ) onde h é a deflexão total desse cabo do jeito que está, além de saber que a distância da corda vale 21   m .

A equação da catenária em A vale:

y a = T 0 μ   cosh ⁡ μ x A T 0 - 1   ( 2 )

A equação da catenária em B vale:

y a + h = T o μ cosh ⁡ μ x a + 20 T o - 1   ( 3 )

Agora fazendo a diferença do ponto B até o ponto A temos:

s b - s a = T 0 μ sinh ⁡ μ x b T 0 - sinh ⁡ μ x a T 0 = T 0 μ sinh ⁡ μ x a + 20 T 0 - sinh ⁡ μ x a T 0 = 21

T 0 μ sinh ⁡ μ x a + 20 T 0 - sinh ⁡ μ x a T 0 = 21           ( 4 )

Passo 4

4 equações, quatro incógnitas. Dá para resolver mas é bem trabalhoso. O recomendado é fazer essa conta com uma ferramenta gráfica.

Se juntarmos a equação 2 em 1 temos:

T 0 1 + cosh ⁡ μ x A T 0 - 1 t g - 1 sinh ⁡ μ x A T 0 = W 2

Comparando agora com a 4 :

T 0 μ sinh ⁡ μ x a + 20 T 0 - sinh ⁡ μ x a T 0 = 21

Temos apenas duas incógnitas agora. Sabendo que μ = 11.772 .

Plotando o gráfico das duas funções nós encontramos

T 0 = 1162.35   N   ;     x a = 20.537       e m   W = 490.5

Logo os valores de y e h serão:

y = T 0 μ   cosh ⁡ μ x A T 0 - 1 = 2.14

h = T o μ cosh ⁡ μ x a + 20 T o - 1 - y = 6.295   m

Link: https://www.desmos.com/calculator/smrhui6kyv

Onde y = T 0 no gráfico ta?

Para W = 0   encontramos:

x a = 0   ; T 0 = 433.04   N

Link: https://www.desmos.com/calculator/cbhzztehai

Logo:

y = 0

h = 5.57   m

Logo a diferença entre as deflexões será o δ que queremos:

δ = 6.295 - 5.57 = 0.725   m

Resposta

δ = 0.725   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma corda de 40m de comprimento está suspensa entre dois pontos que estão separados por uma distância horizontal de 10 m. Calcule a distância h até o ponto mais baixo da corda.
Sob vento fraco, o dirigível está amarrado ao guincho no solo por 100 m de um cabo de 12 m m que tem uma massa de 0,51 k g / m . Um torque de 400N no tambor é necessário para iniciar o enrolamento do
Uma equipe de instalação de cabos quer estabelecer a dependência da força de tração T com a deflexão h do cabo. Faça um gráfico tanto da força trativa mínima T 0 quanto da força tativa T nos apoios A
O cabo do problema 5/163 foi agora colocado sobre os suportes A e B cuja elevação difere de 9m, como mostrado. Faça um gráfico tanto da força trativa mínima T 0 quanto da força tativa T nos apoios A e
Ao se preparar para limpar uma parede com um jato de agua, uma pessoa segura a mangueira conforme mostrado na figura. A mangueira está na horizontal em A e tem uma massa de 0,75k g / m quando está vaz