Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 165
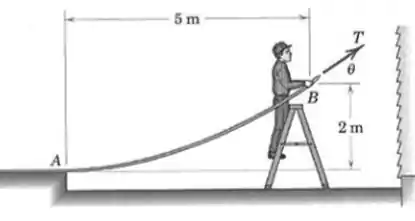
Ao se preparar para limpar uma parede com um jato de agua, uma pessoa segura a mangueira conforme mostrado na figura. A mangueira está na horizontal em A e tem uma massa de quando está vazia e de quando está cheia de água. Determine a força de tração e o ângulo necessários para a mangueira vazia e para a mangueira cheia.
Passo 1
Primeiro vamos anotar as informações que a questão anterior e a imagem nos oferecem, para facilitar a visualização:
Passo 2
Da equação 5/19 temos que:
Solução numérica:
Considerando que:
(cheia ou vazia)
Passo 3
Sabemos então que:
= 63 N vazia
= 105 N cheia
(para y = 2 m)
Resposta
Exercícios de Livros Relacionados
A torre é mantida no lugar pelos três cabos. As forças em cada cabo que atuam sobre a torre estão indicadas na figura. Determine a intensidade e os ângulos de direção coordenados α , β , γ da foça res
Dois cabos são usados para segurar o mastro guincho na posição e sustentar a carga de 1500 N. Se a força resultante é direcionada ao longo do mastro do ponto A para O , determine os valores de x e z p
O cabo conectado aos mastros de uma grua exerce uma força sobre a grua de F = 1,75 kN. Expresse essa força como um vetor cartesiano.
A chapa cilíndrica está submetida às três forças dos cabos que são concorrentes no ponto D . Expresse cada força que os cabos exercem na chapa como um vetor cartesiano e determine a intensidade e os â
Uma força de F = 80N é aplicada no cabo da chave. Determine o ângulo θ entre a origem da força e o cabo da chave A B .