Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 6.Problemas - Ex. 102

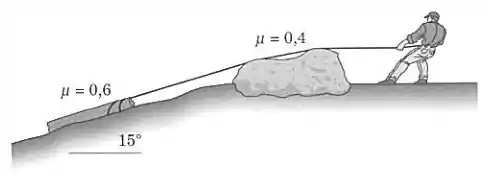
Com que força horizontal o trabalhador deve puxar para mover a tora de 35 kg para cima na inclinação com 15°? O coeficiente de atrito entre a tora e a inclinação vale 0,60 e entre a corda e a rocha vale 0,4.

Passo 1

Para puxar a corda, o trabalhador deve fazer uma força que se iguale à força de atrito entre a corda e a rocha mais a força de tração feita pela tora. A fórmula para o equilíbrio de uma corda em volta de uma superfície é dada por:

Sendo e as trações maior e menor nas extremidades da corda, o coeficiente de atrito entre a corda e a superfície e o ângulo total de giro da corda. Como a fórmula não envolve um raio específico, a superfície não precisa ser circular (como numa polia), e esse ângulo nesse caso é igual a 15°. Através dessa fórmula, seremos capazes de achar a força .

Passo 2

Temos o coeficiente de atrito entre a corda e a rocha, e o ângulo . A tração é a força que o trabalhador deve fazer, então precisamos primeiro encontrar o valor da tração menor feita na tora para aplicar a fórmula e achar . Achamor através do equilíbrio da tora, então vamos representá-la em diagrama de corpo livre. Há três forças atuando nela: o peso , a tração e a força feita pelo solo. Pelo equilíbrio do corpo, as três forças devem ser concorrentes no mesmo ponto, o centro de massa.

Colocando o eixo paralelo ao plano inclinado, podemos achar pelo equilíbrio nas direções e das forças na tora. Sabe-se que a força feita pelo solo, composta por normal e atrito, deve fazer com a linha normal à superfície de contato um ângulo , o ângulo de atrito, tal que:

Sendo o atrito entre a tora e o solo. Então achamos o ângulo :

Primeiro vamos fazer a soma das forças na direção normal ao solo, pois não aparece e achamos diretamente . A massa da tora é de 35 kg:

Agora fazemos o equilíbrio das forças na direção :

Passo 3

Agora que temos a tração na extremidade esquerda da corda, já possuímos todos os valores necessários para achar na equação de equilíbrio. Então substituímos os valores. O ângulo deve ser colocado em radianos, então multiplicamos por :