Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 5.Problemas - Ex. 185

174- Um béquer com água doce está em uma balança quando o peso de aço inoxidável de 1   k g é colocado no béquer. Qual é a força normal que o peso exerce sobre o fundo do béquer? De quanto aumenta a leitura da balança, quando o peso é adicionado? Explique a sua resposta.

Passo 1

Inicialmente a balança marca somente o peso da água, quando o peso é colocado a normal do conjunto todo sobe 1   k g × 9.81 = 9.81   N porém a contribuição do peso de 1   k g a esse sistema não é de 9.81   N pois a água exerce um empuxo a esse corpo influenciando na normal do peso, o que altera para equilibrar esse sistema é que a pressão da água aumenta ao subir de nível.

Passo 2

Vamos fazer o diagrama de forças no bloco:

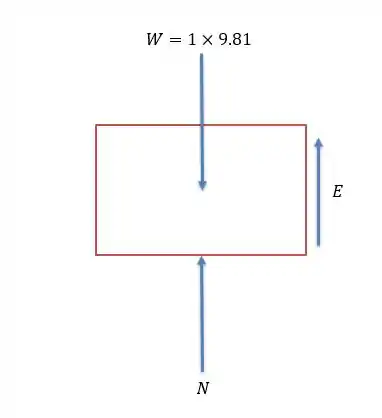
Onde o empuxo E pode ser calculado por:

E = ρ l i q u i d o × g × V

Porém o volume do corpo pode calculado por:

ρ c o r p o = m V → V = m ρ c o r p o

O que nos deixa com um empuxo com:

E = ρ l i q u i d o ρ c o r p o × m g

Pela tabela no anexo D desse livro temos que a densidade da água doce valerá 1000   k g / m 3 enquanto a do aço valerá 7830   k g / m 3 . Logo a força de empuxo valerá:

E = 1000 7830 × 1 × 9.81 = 1.253   N

Passo 3

Então a normal exercida pelo peso será (pela somatória das forças verticais):

N - 9.81 + 1.253 = 0 → N = 8.557   N   ( p a r a   b a i x o )

Resposta

Peso adicionado: 9.81   N

Normal exercida pelo bloco: 8.557   N

Explicação do passo 1 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se F 1 = 150 N e ϕ = 30 ° , determine a intensidade da força resultante que atua sobre o suporte e sua direção, medida no sentido horário a partir do eixo positivo x .
As três forças concorrentes que atuam sobre o poste produzem uma força resultante F R = 0 . Se F 2 = 1 2 F 1 e F 1 estiver a 90 ° de F 2 , como mostra a figura, determine a intensidade necessária de F
Se a intensidade da força resultante que atua sobre o suporte deve ser 450N direcionada ao longo do eixo u positivo, determine a intensidade de F 1 e sua direção ϕ .
Especifique a intensidade de F 3 e seus ângulos de direção coordenados α 3 , β 3 , γ 3 de modo que a força resultante seja F R = { 9 j } kN.
2.6. Se a força F precisa ter uma componente ao longo do eixo u com F u = 6k N , determine a intensidade de F e de sua componente F v ao longo do eixo v.