Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 3.Problemas - Ex. 111

Cada uma das três barras uniformes de 1200   m m tem uma massa de 20   k g . As barras estão soldadas juntas na configuração mostrada e estão suspensas por três arames verticais. As barras A B e B C estão no plano horizontal x - y e a terceira barra está em um plano paralelo ao plano x - z . Calcule as forças trativas em cada arame.

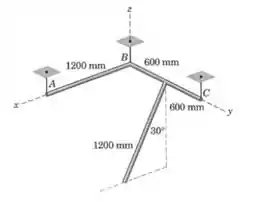
Passo 1

Vamos começar desenhando as forças que agem sobre o sistema:

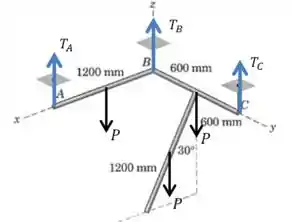
Nós já podemos calcular a força P , que é igual nos três casos:

P = 20 9,81 = 196,2   N

Mas as forças T A , T B e T C são desconhecidas. Precisamos montar equações de equilíbrio de forma que duas dessas variáveis não apareçam em cada equação.

Passo 2

Começamos com o momento em relação ao eixo x . Nesse caso eliminamos as forças T A e T B , que cruzam o eixo, e uma das forças P :

∑ M x = 0

E as outras duas forças P está a uma distância perpendicular de 600   m m do eixo x :

∑ M x = T C 600 + 600 - ( 2 ) ( P ) ( 600 )

T C = 2 196,2 600 ( 600 + 600 ) = 196,2   N

Passo 3

Agora, seguindo a mesma lógica, vamos ver o momento em relação ao eixo y :

∑ M y = 0

Nesse caso restam apenas T A e duas das forças P . Dessa vez, a distância da força P que age sobre a barra inclinada até o eixo y é 600 cos ⁡ 60 ° :

∑ M y = T A 1200 - P 600 - P 600 cos ⁡ 60 ° = 0

T A = 196,2 600 + 196,2 600 cos ⁡ 60 ° 1200 = 147,15   N

E encontramos o ângulo de 60 ° fazendo 90 ° - 30 ° = 60 ° .

Passo 4

Agora que sobrou apenas uma variável desconhecida, vamos usar uma equação de equilíbrio mais simples, a do equilíbrio das forças na direção z :

∑ F z = 0

∑ F z = T A + T B + T C - 3 P

147,15 + T B + 196,2 - 3 196,2 = 0

T B = 3 196,2 - 196,2 - 147,15

T B = 245,25   N

E então (arredondando), as três forças são:

T A = 196,2   N

T B = 245,2   N

T C = 147,2   N

Resposta

As três forças são T A = 196,2   N , T B = 245,2   N , T C = 147,2   N .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se o peso do mastro é desprezível comparado à carga de 30k N aplicada, determine as forças trativas T 1 e T 2 nos cabos e a força atuando na rótula em A .
Determine a força trativa T necessária para manter o sólido retangular na posição mostrada. O sólido retangular com 125k g é homogêneo. O atrito em D é desprezível.
O braço curvo B C e os cabos A B e A C presos a ele sustentam uma linha de transmissão, que está situada no plano vertical y - z . As tangentes à linha de transmissão, na posição do isolante abaixo de
Uma força vertical P no pedal do dispositivo é necessária para produzir uma força trativa T de 400N na barra de controle vertical. Determine as reações correspondentes nos mancais em A e B .