Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 51
Se N e , determine a intensidade da força resultante que atua sobre o suporte e sua direção, medida no sentido horário a partir do eixo positivo .
Passo 1
Falaa! Ele quer a intensidade da força resultante e a orientação dela em relação a no sentido horário. Lembra que
Aí o que a gente pode fazer é achar a componente e a da resultante que a gente quer achar, ao calcular a soma das componentes das forças em e .
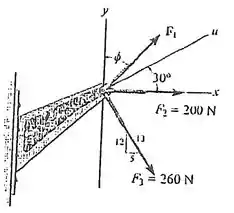
Vamos começar achando essas componentes. Veja que está sobre o eixo no sentido positivo, então essa já sua componente e é zero:
Para achar as componentes de , precisamos observar que o ângulo de orientação está colado em , isso quer dizer que vamos multiplicar nossa força por cosseno para achar a componente de e por seno para achar a componente de . Fica ssim:
Passo 2
Para achar as componentes de vamos usar o triângulo que ele dá como orientação da força.
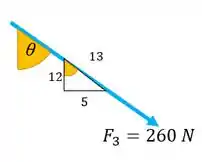
Aí temos o ângulo colado em de novo, então as componentes ficam:
Repara que a componente em fica com sinal de menos porque ela está no sentido negativo de .
Para achar esse cosseno e esse seno a gente usa o triângulo
Aí temos
Passo 3
Aí somando as componentes em , achamos
Agora somando as componentes em :
Passo 4
Sendo assim, a intensidade da força resultante é:
Passo 5
Por último encontramos a direção pelo ângulo no sentido horário de . Vamos representar vetorialmente a situação
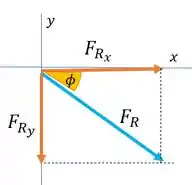
Repare que da representação vetorial podemos extrair o seguinte triângulo
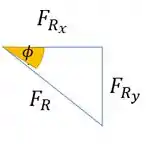
E para determinar , basta lembrar que
Obs: aqui a gente usou positivo porque já tínhamos levado o quadrante em consideração para formar o triângulo.