Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 18
18- O pino em é preso ao elemento e pode deslizar ao longo de uma fenda aberta na placa fixa mostrada na figura. Desprezando o efeito do atrito, deduza uma expressão para a intensidade do binário necessária para se manter o equilíbrio quando a força atuante em está direcionada tal como mostra a figura, verticalmente para para baixo, horizontalmente para a direita.
Passo 1
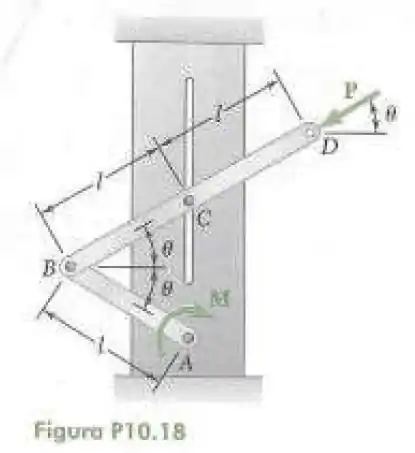
Para a letra conseguimos ver que o momento de tende a diminuir o ângulo na barra gerando um trabalho virtual de
Agora precisamos encontrar uma relação de trabalho que faz com e a melhor forma de se colocar o eixo de coordenadas é onde se tem a aplicação do momento que é em , da seguinte forma:
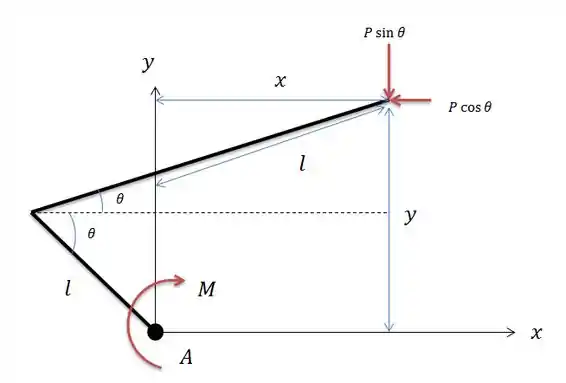
Qualquer outra força como a presente em não gera trabalho então não se considera esse tipo de força.
Passo 2
Analisando a figura temos que:
E como ambas as forças de projetadas nos eixo e tendem a diminuir esses deslocamentos virtuais , o que gera trabalhos virtuais positivos então o trabalho virtual total para a letra a será:
Passo 3
Na letra temos apenas a força vertical para baixo nos dando a seguinte somatória de trabalhos virtuais:
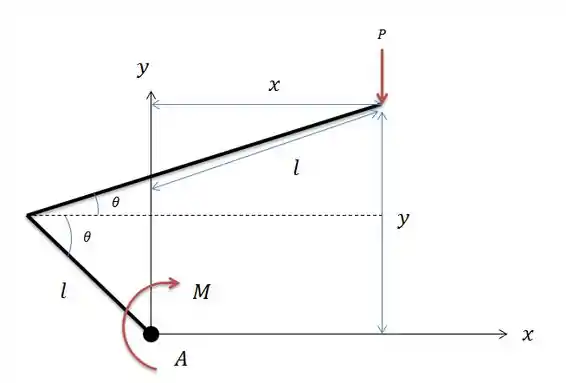
Passo 4
Agora a somatória de trabalhos virtuais para uma força apontada somente para a direita:
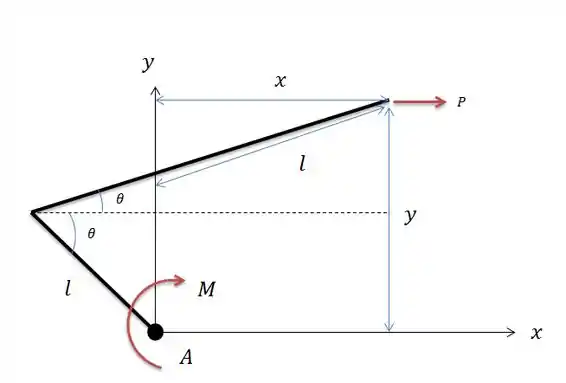
Pois essa força tende a esticar a linha de trabalho de valor igual a , sendo um trabalho negativo.