Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 11.Problemas - Ex. 11
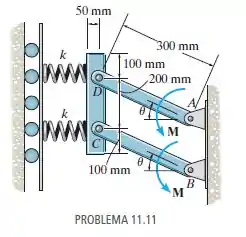
Quando , o bloco uniforme de comprime as duas molas horizontais em . Determine a intensidade dos momentos de binário aplicados necessários para manter o equilíbrio. Considere e despreze a massa das conexões.
Passo 1
Oi, tudo bem? Vamos resolver este exercício.
A distância horizontal do ponto fixo ao ponto onde a força da mola está atuando vale:
Portanto:
A distância vertical é dada por:
Portanto:
Passo 2
Aplicando o principio do trabalho virtual, temos que:
Substituindo os valores, temos que:
Portanto, temos que:
Resposta
Exercícios de Livros Relacionados
Se a carga F pesa 100N e o bloco G pesa 10N , determine sua posição x para o equilíbrio da balança diferencial. A balança está em equilíbrio quando a carga e o bloco não estão na balança.
A placa de ventilação é apoiada em B por um pino. Se ela pesa 75N e tem um centro de gravidade em G , determine a rigidez k da mola de modo que a placa permaneça em equilíbrio em θ = 30 ° . A mola est
Uma força horizontal W de intensidade de 324 N é aplicada ao mecanismo em C. Desprezando o peso do mecanismo, determine o valor de θ correspondente ao equilíbrio. A constante da mola é k = 3.6k N / m
Duas hastes AC e CE são unidas por um pino em C e por uma mola AE. A constante da mola é 270 N/m, e a mola está indeformada quando θ = 30 ° . Sabendo que l = 250m m e desprezando os pesos das hastes,
Uma força vertical W é aplicada ao mecanismo articulado em B. A constante da mola é k, e a mola está indeformada quando AB e BC são horizontais. Desprezando o peso do mecanismo, deduza uma equação em