Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas - Ex. 45
18.45. Determine a energia cinética do corpo do Problema 18.19.
Passo 1
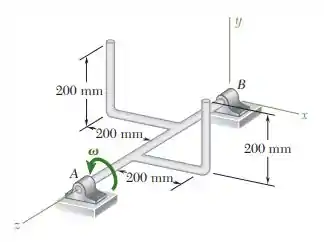
Vamos relembrar o problema 18.19. Temos dois braços no formato de L e cada um tem a massa de , eles estão soldados na barra de que está girando à , ou . Cada comprimento das barras em L mede .
Nós podemos calcular a energia cinética com a equação:
Já que só temos velocidade angular no eixo z.
Passo 2
Agora vamos separar a nossa figura em quatro segmentos e calcular o momento de inércia em relação ao eixo z de cada um. Cada segmento que vamos calcular aqui é uma parte de uma das barras L.
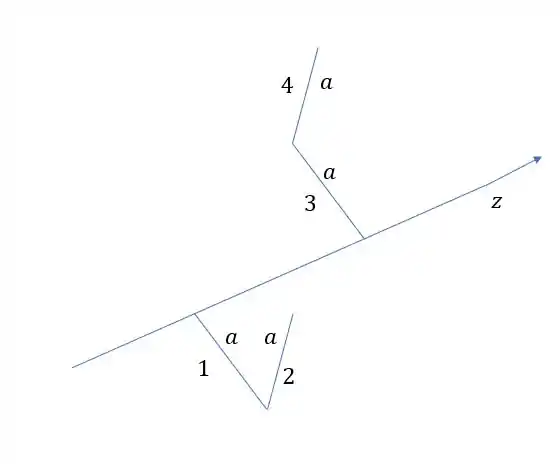
Vamos ver como fica o momento em cada parte
Agora é só a gente somar tudo
Passo 3
Então a energia cinética fica
Substituindo os valores
Resposta
Exercícios de Livros Relacionados
Um pedaço de chapa de aço de 2,4 kg com dimensões 160 mm x 640 mm foi dobrada na forma do componente mostrado na figura. Ocomponente está em repouso ( ω = 0 ) quando o binário M 0 = 0,8N ∙ m K é aplic
Determine a energia cinética perdida quando o disco do Problema atinge a obstrução em B.
Um concentrador experimental de energia solar por lentes Fresnelpode girar em torno do eixo horizontal AB que passa por meio deseu centro de massa G. Ele é suportado em A e B por uma estruturaque pode
Uma hélice de quatro lâminas de um avião tem massa de 160 kg e raio de giração de 800 mm. Sabendo que a hélice gira a 1.600 rpm quando o avião voa em uma trajetória circular vertical de 600 m de raio
A engrenagem A de 950 -g é restrita a rolar na engrenagem fixa B, mas é livre para girar em torno do eixo AD. O eixo AD, de comprimento 400 mm e massa desprezível, é conectado por uma manilha ao eixo