Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas - Ex. 46

18.46. Determine a energia cinética transmitida para o cubo do Problema 18.21.

Passo 1

Vamos relembrar o problema 18.21. Um cubo oco feito com alumínio, onde cada face tem 2 × 2   m de comprimento, está soldado numa base fica e pode girar livremente sobre sua diagonal principal A B .

Vamos escolher um sistema de coordenadas de forma que os eixos sempre sejam perpendiculares as faces do cubo, dessa forma vai ser mais fácil para gente.

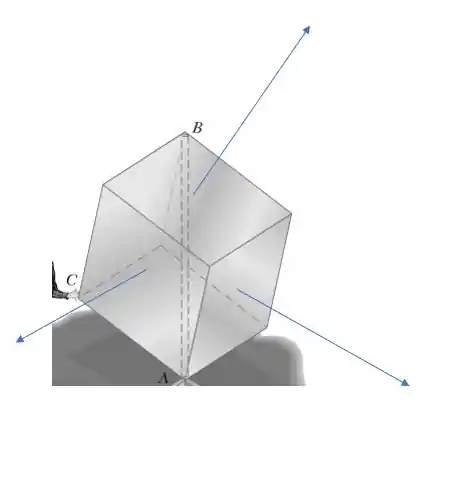
Passo 2

A simetria do cubo vai ajudar bastante a gente aqui. O cubo tem 6 faces, vamos determinar o momento de inércia de cada uma. Para as faces perpendiculares ao eixo x , temos

I x 1 = 1 6 m a 2

Sendo a o tamanho da lateral do cubo.

E para as faces perpendiculares aos eixos y e z

I x 2 = 1 12 + 1 4 m a 2 = 1 3 m a 2

Então o momento de inercia total é

I x = 2 ⋅ I x 1 + 4 ⋅ I x 2 = 1 3 m a 2 + 4 3 m a 2 = 5 3 m a 2

E como estamos tratando de um cubo no problema, existe uma simetria maravilhosa que nos permite dizer que

I x = I y = I z

Olha só que coisa boa!

E isso vai trazer umas simplificações para a gente, porque isso significa que todos os eixos centroidais são eixos principais.

Passo 3

Se usarmos o princípio de impulso-momento, temos

b F Δ t = H y

Então

b F Δ t = 5 3 m a 2 ω

Ou seja

m = 3 5 b F Δ t ω a 2

Dado a = 2   m , então b = 2 3 2 = 1,633   m . Calculamos b com a dica do problema.

ω = 2 π 5 = 1,2566 r a d s

F = 60   N

E

Δ t = 1,2   s

Então

m = 3 5 ( 1,663 ) ( 60 ) ( 1,2 ) 1,2566 2 2 = 14,3   k g    

Passo 4

Agora que temos a massa basta fazer

T = 1 2 I x ω x 2 + I y ω y 2 + I z ω z 2

Então

T = 1 2 I y ω y 2

Substituindo os valores

T = 1 2 5 3 m a 2 ω 2

T = 1 2 5 3 14,3 2 2 1,2566 2 = 75,27   J

Resposta

T = 75,27   J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um disco homogêneo de raio ae massa é suportado por uma junta esférica em A está girando em torno de seu diâmetro vertical com uma velocidade angular constante para ω = ω 0 j quando uma obstrução é re
Uma haste uniforme de massa me comprimento 5a é dobrada na forma mostrada e é suspensa de um fio preso em B. Sabendo que a haste é atingida em C na direção z negativa e denotando o impulso corresponde
O disco fino de massa m = 4 kg gira com uma velocidade angular ω 2 em relação ao braço OA, que por sua vez gira com uma velocidade angular ω 1 em torno do eixo y. Determine (a) o binário M 1j , que po
Um anel fino de 100 mm de raio é preso por um cursor em A a umeixo vertical que gira com uma velocidade angular constante ω . Determine (a) o ângulo constante que o plano do anel forma com avertical q
Um disco de 2 kg e 150 mm de diâmetro está preso na extremidadede uma barra AB de massa desprezível que é suspensa por junta articulada em A. Se no disco for observada a precessão em torno da vertical