Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas - Ex. 58

18.58. Determine a taxa de variação G da quantidade de movimento angular HG do disco do Problema 18.4, admitindo que, no instante considerado, o conjunto tenha uma velocidade angular j e uma aceleração angular α j.

Passo 1

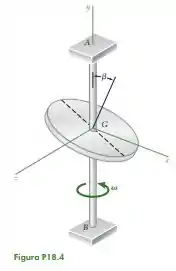
Beleza vamos para mais uma questão. No problema 18.4 temos um disco homogêneo de massa m e raio r está montado em um eixo vertical AB, com a normal formando um ângulo β = 25 ° , com o eixo. A velocidade do eixo é constante igual a ω → = ω   j ^ .

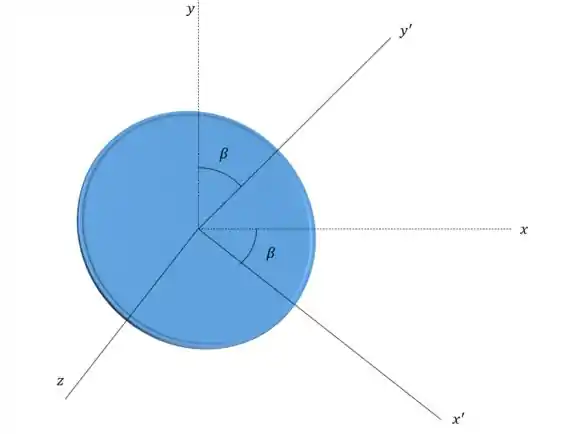
Para esse problema vamos precisar usar os eixos principais G x ' y ' z ' .

E

z ' = z

Passo 2

O próximo passo é calcular os momentos de inércia:

I x ' = 1 4 m r 2 + 1 12 m L 2

Sendo L a espessura do disco, mas para esse problema podemos desprezar essa espessura, então

I x ' = 1 4 m r 2

Analogamente

I z ' = 1 4 m r 2

E por último

I y ' = 1 2 m r 2

E vamos converter a velocidade angular para os novos eixos:

ω x ' = - ω ⋅ sin ⁡ β ω y ' = ω ⋅ cos ⁡ β ω z ' = 0

Passo 3

Agora temos tudo para calcular o momento angular em torno do ponto G.

H → G = H x '   i ^ ' + H y '   j ^ ' + H z ' k ^ '

Isso fica

H → G = I x ' ω x '   i ^ ' + ( I y ' ω y ' )   j ^ ' + I z ' ω z ' k ^ '

Substituindo os valores dos momentos inércia e velocidade angular:

H → G = 1 4 m r 2 ⋅ - ω ⋅ sin ⁡ β   i ^ ' + 1 2 m r 2 ⋅ ω ⋅ cos ⁡ β   j ^ ' + 1 4 m r 2 ⋅ 0 k ^ '

Ou seja

H → G = - 1 4 m r 2 ω sin ⁡ β i ^ ' + 1 2 m r 2 cos ⁡ β   j ^ '

H → G = m r 2 ω - 1 4 sin ⁡ β   i ^ ' + 1 2 cos ⁡ β   j ^ '

Agora vamos converter isso para os eixos cartesianos:

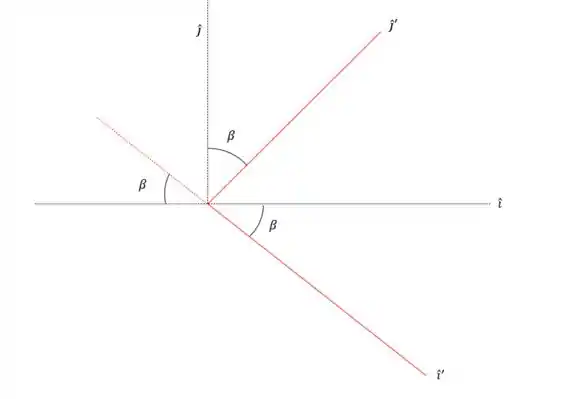
Olha só para a imagem, nós podemos dizer que:

i ^ ' = cos ⁡ β   i ^ - sin ⁡ β   j ^

E

j ^ ' = sin ⁡ β   i ^ + c o s   β   j ^

Então para convertemos para os eixos cartesianos basta fazer

H → G = m r 2 ω - 1 4 sin ⁡ β   cos ⁡ β   i ^ - sin ⁡ β   j ^ + 1 2 cos ⁡ β sin ⁡ β   i ^ + c o s   β   j ^

Isso fica

H → G = m r 2 ω - 1 4 sin ⁡ β cos ⁡ β   i ^ + 1 4 sin 2 ⁡ β   j ^ + 1 2 cos ⁡ β sin ⁡ β i ^ + 1 2 cos 2 ⁡ β j ^

H → G = m r 2 ω 1 4 sin ⁡ β cos ⁡ β   i ^ + 1 4 sin 2 ⁡ β   + 1 2 cos 2 ⁡ β j ^

Assumindo β = 25 °

H → G = m r 2 ω 0,09575   i ^ + 0,455348   j ^

Passo 4

Agora vamos podemos calcular H → ˙ A , e isso não vai ser tão complicado nesse problema, porque ω é constante, então

H → ˙ G x y z = 0

E também podemos assumir

Ω → = ω → = ω   j ^

Então

H → ˙ A = H → ˙ G x y z + Ω → × H A →

É a mesma coisa que

H → ˙ A = ω → × H A →

Substituindo os valores

H → ˙ A = ω   j ^ × m r 2 ω 0,09575   i ^ + 0,455348   j ^

Agora é só fazer esse produto vetorial

H → ˙ A = - 0,958   m r 2 ω 2   k ^

E assim terminamos mais um problema.

Resposta

H → ˙ A = - 0,958   m r 2 ω 2   k ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um colar com uma massa de 1 kg é rigidamente preso a uma distância d = 300 mm da extremidade de uma haste fina e uniforme AB. A haste tem uma massa de 3 kg e é de comprimento L = 600 mm. Sabendo que a
O berço de 9 kg é suportado como mostrado por dois discos uniformes que rolam sem deslizar em todas as superfícies de contato. A massa de cada disco é m = 6 kg e o raio de cada disco é r = 80 mm. Sabe
Uma meia seção do tubo de massa m e raio r é liberada do repouso na posição mostrada. Sabendo que o tubo rola sem deslizar, determine (a) sua velocidade angular depois de ter rolado 90 °, (b) a reação
Dois cilindros uniformes, cada um com peso W = 14 lb e raio r = 5 pol., são conectados por uma correia, conforme mostrado. Sabendo que a velocidade angular inicial do cilindro B é de 30 rad / s no sen
O berço de 9 kg é apoiado conforme mostrado por dois discos uniformes que rolam sem deslizar em todas as superfícies de contato. A massa de cada disco é m = 6 kg e o raio de cada disco é r = 80 mm. Sa