Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.9 - Ex. 188

188- Uma esfera sólida e homogênea de raio r está apoiada sobre o fundo de um tanque que contém um líquido de massa específica ρ l , que é maior do que a massa específica ρ s da esfera. A medida que o tanque é enchido, uma altura h é atingida, na qual a esfera começa a flutuar. Determine a expressão para a massa específica ρ s da esfera.

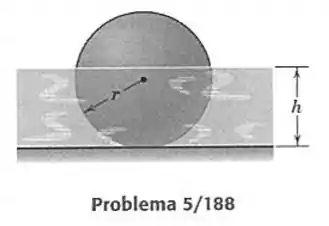
Passo 1

O sistema é equilibrado pelas duas forças presentes no sistema que são:

P = E

O peso P da esfera e o empuxo E imposta pelo líquido na bola.

O peso da esfera é fácil de calcular e vale:

P = m g = ρ c o r p o g V c o r p o = ρ s g × 4 3 π r 3

P = 4 π ρ s g r 3 3

Passo 2

A dificuldade se encontra quando temos que calcular a força de empuxo pois tem que encontrar o volume submerso na esfera.

E = ρ l g V s u b

Esse volume é o mesmo volume de uma calota esférica e ele é calculado de acordo com a seguinte integral.

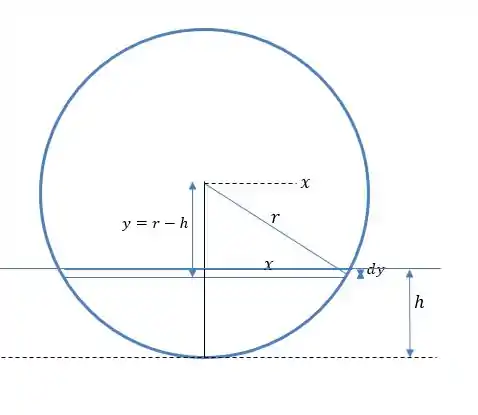
Onde consideraremos um anel de raio x e altura igual a d y   quer terá volume igual a:

d V = π x 2 d y

Onde x é um dos catetos do triângulo retângulo formado entre r e y , x valerá:

x 2 + y 2 = r 2 → x 2 = r 2 - y 2

Logo o volume desse anel valerá :

d V = π r 2 - y 2 d y

Considerando o eixo da esfera começando no centro da esfera e tendo como valor positivo de y o sentido de cateto y , temos que o intervalo em y que esse anel percorre indo de r até r - h (que são os intervalos inicial e final do y na figura), logo o volume total dessa esfera será:

V = ∫ r - h r π r 2 - y 2 d y

Fazendo a integral temos que o volume dessa calota será de:

V = π r 2 y - y 3 3 r - h r

V = π 3 3 r 2 y - y 3 r - h r

Aplicando o intervalo:

V = π 3 3 r 3 - r 3 - 3 r 2 r - h + r - h 3  

V = π 3 2 r 3 - 3 r 3 + 3 r 2 h + r 3 - 3 r 2 h + 3 r h 2 - h 3

V = π 3 3 r h 2 - h 3

V = π h 2 3 3 r - h

Logo o empuxo na esfera será:

E = π ρ l g h 2 3 [ 3 r - h ]

Passo 3

Igualando as duas forças temos:

π ρ l g h 2 3 3 r - h = 4 π ρ s g r 3 3

Isolando ρ s :

ρ s = ρ l h 2 4 r 3 [ 3 r - h ]

Resposta

ρ s = ρ l h 2 4 r 3 [ 3 r - h ]

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

202- A janela de observação trapezoidal em um aquário de água salgada tem as dimensões mostradas. Com a ajuda dos diagramas e coordenadas apropriados, descreva dois métodos pelos quais a força resulta
204- A determinação exata da posição vertical do centro de massa G de um navio é difícil de ser obtida por cálculo. Ela é mais facilmente obtida por um experimento simples de inclinação do navio carre
2.45. Se a força resultante que atua sobre o suporte precisa ser direcionada ao longo do eixo x positivo e a intensidade de F 1 precisa ser mínima, determine as intensidades da força resultante e de F
O elemento B D exerce sobre o elemento A B C uma força P dirigida ao longo da linha B D . Sabendo que P deve ter um componente horizontal de 1330N , determine (a) a intensidade da força P , (b) sua co
Determine os componentes x e y de cada uma das forças indicadas.