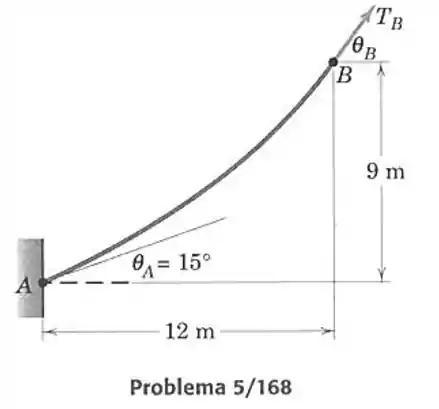
168- Um cabo que tem uma massa de por metro de comprimento está preso ao ponto . Uma força trativa é aplicado ao ponto , fazendo com que o ângulo valha . Determine e .

Utilizando a equação (equação da catenária) no ponto temos que:

Agora temos que entender que o ponto encontra-se em relação ao ponto , o que faz com que a equação no ponto seja:

Agora podemos utilizar a informação de que no ponto temos uma inclinação de ao derivar a equação pertinente a .

Isso é:

Temos três equações para três incógnitas.

Pela terceira equação temos que:

Como logo:

Substituindo na primeira equação temos:

O que faz nós encontrarmos:

Substituindo esses dois resultados na segunda equação:

Resolvendo numericamente essa equação nós encontraremos:

E por consequência:

Agora podemos achar o valor de e do ângulo cabo a uma vez que temos seus valores médios:

Aplicando a equação de resistência do cabo temos:

Para encontrar o ângulo aplicamos o mesmo raciocínio feito no passo :

Uma vez que e