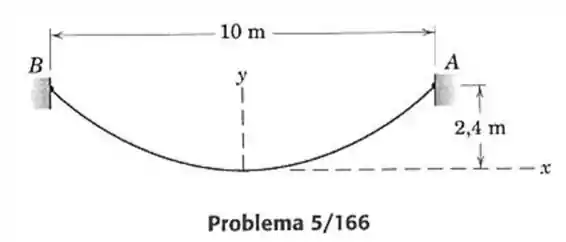
166- Um determinado comprimento de um cabo, que tem uma massa de , deve ter uma deflexão de quando estiver suspenso entre dois pontos e distando sobre a mesma linha horizontal. Para efeito de comparações, determine o comprimento do cabo necessário e faça um gráfico de sua configuração para os dois casos: considerando uma forma parabólica e usando o modelo de catenária apropriado. A fim de distinguir mais claramente entre os dois casos, faça também o gráfico da diferença em função de , onde e se referem a catenária e a parábola, respectivamente.
Passo 1
O peso específico do cabo é dado por:
O ponto de deflexão máxima é de
E a deflexão máxima de
Passo 2
Letra ) Pela equação do arco- parabólico(5/14) conseguimos encontrar que o valor de é:
Logo teremos uma equação parabólica de comportamento do cabo igual a:
Passo 3
Agora para o cálculo do comprimento do arco parabólico temos que fazer uso da equação que nos diz que:
Onde é a maior deflexão do cabo e o comprimento total horizontal do cabo, e como é menor que então essa equação converge para um número. Fazendo a conta:
Logo o tamanho de cabo necessário pela abordagem parabólica é de .
Passo 4
b) Abordagem do cabo catenária
Pela equação temos o valor de igual a:
Substituindo os valores no ponto médio temos:
Numericamente descobrimos um valor de .
Esse valor faz com que tenhamos uma equação igual a:
Passo 5
O comprimento do cabo segundo a abordagem catenária pode ser dada por:
Esse é o comprimento total do cabo que tem estar disponível.
Passo 6
Gráficos de e
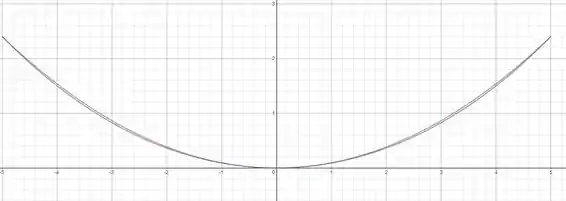
Onde a curva azul é da catenária e a vermelha da parabólica.
Gráfico de .
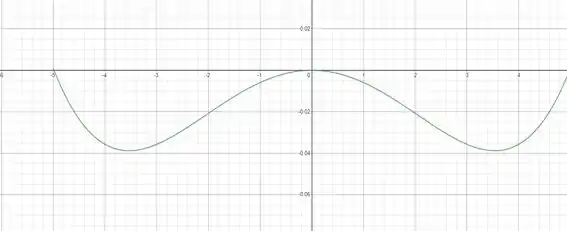
Resposta
- e
- e
Gráficos do passo .