Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.9 - Ex. 189
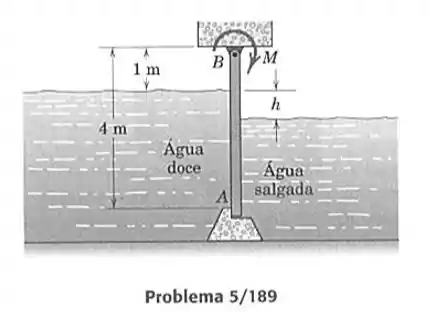
189- A comporta retangular, mostrada em seção, tem de comprimento (perpendicular ao plano do papel) e bascula em relação a sua borda superior . A comporta divide um canal, que a esquerda leva a um lago de água doce, e á direita a uma bacia de água do mar preenchida pela maré. Calcule o torque no eixo da comporta, em , necessário para prevenir que a comporta abra quando o nível de água do mar cai para .
Passo 1
Vamos desenhar o sistema de forças e momentos agindo para entendermos melhor o que está acontecendo.
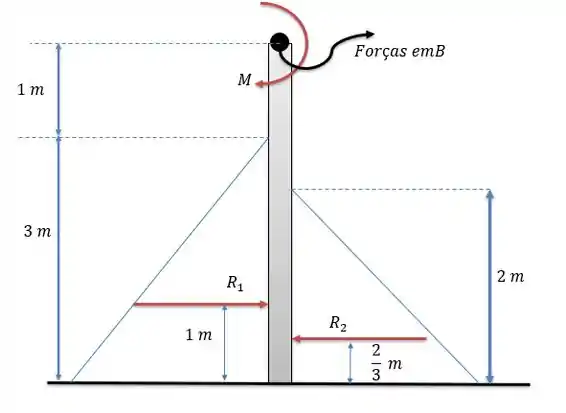
A área da comporta reagindo a água doce é de e seu centroide vertical estará em .
Para a água salgada a área da comporta será de e sua altura média estará em
Logo a força causada pela água salgada é de:
E a causada pela água doce será de:
Passo 2
Agora podemos encontrar o momento ao se somar todos os momentos presentes em .
Considerando o sentido horário como positivo temos: