Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 27
O cabo de sustentação exerce no poste telefônico uma força dirigida ao longo de . Sabendo que tem uma componente de perpendicular ao poste , determine (a) a intensidade da força , (b) sua componente ao longo da linha .
Passo 1
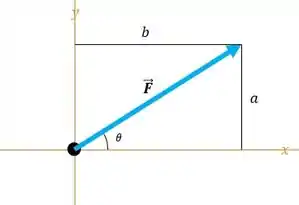
Bom galera, a gente vai encontrar as componentes horizontais e verticais de cada uma das forças que é dada por:
Passo 2
Show de bola, a gente também sabe que a componente perpendicular ao poste vale e fica na direção do eixo , então usando a trigonometria para essa componente temos:
Passo 3
Por último, a gente calcula a componente pararela ao poste que fica no eixo :
Resposta
Exercícios de Livros Relacionados
Uma força horizontal de 50N é aplicada à alça da válvula de água industrial, conforme mostrado. A força é perpendicular ao plano vertical contendo a linha O A - do punho. Determine o sistema de força-
Determine o ângulo θ o qual irá maximizar o momento M 0 da força de 50l b ao redor do eixo em O . Calcule também o momento M 0 .
Uma força de 50l b é aplicada ao pedal de controle, conforme mostrado. A força encontra-se em um plano paralelo ao plano x - z e é perpendicular a B C - . Determine os momentos desta força sobre o pon
A linha de força é amarrada do braço do pólo de força em A ao ponto B no mesmo plano horizontal. Por causa da curvatura do cabo no plano vertical, o cabo faz um ângulo de 15° com a horizontal onde se
Como parte de um teste de projeto, a roda dentada de acionamento do eixo de comando é fixada e, em seguida, as duas forças mostradas são aplicadas a uma correia enrolado em torno da roda dentada. Enco