Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.9 - Ex. 191

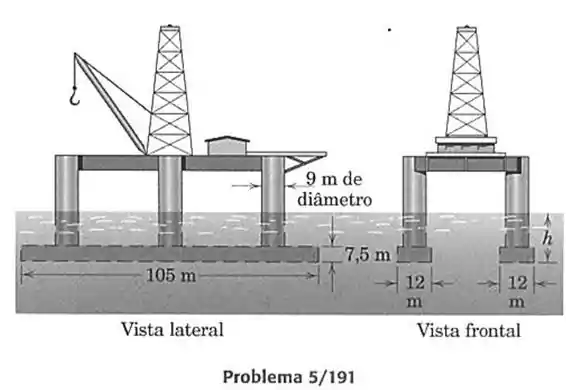
191- O projeto de uma plataforma flutuante de perfuração de petróleo consiste em dois flutuadores retangulares e em seis colunas cilíndricas, que suportam a plataforma de trabalho. Quando lastreada, a estrutura como um todo tem um deslocamento de 26000 toneladas métrica (1 tonelada métrica é igual a 1000   k g ). Calcule a altura total submersa h da estrutura quando ela é ancorada no oceano. A massa específica da água salgada é de 1030   k g / m 3 . Despreze as componentes verticais das forças de ancoragem.

Passo 1

O volume submerso dessa plataforma pode ser calculado por:

V = 2 × 105 × 7.5 × 12 + 6 × π × 9 2 2 × ( h - 7.5 )

Onde se calcula a área dos dois flutuadores com formato de paralelepípedo e dos seis cilindros de altura igual a h subtraído de 7.5   do flutuador:

V = 18900 + 381.7 ( h - 7.5 )

Passo 2

O diagrama de forças desse sistema nos daria que o peso da estrutura toda tem que se equilibrar com o empuxo da água, como a massa de tudo é de 26 × 10 6   k g temos a seguinte equação:

P = E

26 × 10 6 × 9.81 = 1030 × 9.81 × 18900 + 381.7 h - 7.5

26 × 10 6 = 19.467 × 10 6 + 393151 ( h - 7.5 )

6.533 × 10 6 39315 = h - 7.5

h = 24.12   m

Resposta

h = 24.12   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cilindro hidráulico B D exerce sobre o membro A B C uma força P dirigida ao longo da linha B D . Sabendo que P tem uma componente perpendicular a A B C de 750N , determine (a) a intensidade da forç
Para o anel do Problema 2.36, determine (a) a tração necessária no cabo B C se a resultante das três forças exercidas no ponto B seja vertical, (b) a correspondente intensidade da resultante.
Para o bloco dos Problemas 2.37 e 2.38, determine (a) o valor necessário de α para que o resultante das três forças mostradas seja paralela ao plano inclinado, (b) a correspondente intensidade da resu
Para o anel do Problema 2.35, determine (a) o valor necessário de α para que a resultante das forças seja na vertical, (b) a correspondente intensidade da resultante.
Determine (a) a tensão de tração necessária no cabo A C , sabendo que a resultante das três forças exercida no ponto C da haste B C seja ao longo da linha B C . (b) a correspondente intensidade da res