Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 41
Determine (a) a tensão de tração necessária no cabo , sabendo que a resultante das três forças exercida no ponto da haste seja ao longo da linha . (b) a correspondente intensidade da resultante.
Passo 1
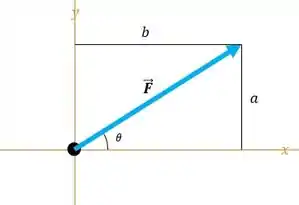
Bom galera, a gente vai encontrar as componentes horizontais e verticais de cada uma das forças que é dada por:
Passo 2
Show de bola, a gente quer a resultante atuando na linha de , então para isso vamos considerar a linha o eixo , e como a força atua apenas nesse eixo, então:
Passo 3
Por último, a gente calcular a soma das componentes na linha , porque a resultante atuará apenas nessa linha:
Resposta
Exercícios de Livros Relacionados
Sabe-se que a força F da componente y exerce 90N no pino P , quando θ=30 ° e β=15 ° . Determine o módulo de força F e as componentes xd eF .
Um cabo esticado entre o suporte fixo AeB está sob uma tensão trativa de 2k N . Expresse a tensão como um vetor usando, os vetores unitários iej , primeiro, e como uma força T A atuando em A e como um
As três forças atuam perpendiculares à placa retangular, como mostrado. Determine os momentos M 1d eF 1 ,M 2d eF 2eM 3d eF 3 , todos em relação ao ponto O .
Substitua as três forças mostradas por um sistema força-binário equivalente no pontoA . Determine a distância d abaixo do ponto A em sua linha de ação, se as forças forem substituídas por uma força re
Quatro forças atuam no olhal, como mostrado. Se o efeito resultante delas sobre o parafuso é um esforço trativo de 3k N na direção x , determine os valores necessários de θeT .