Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 40
Para o anel do Problema 2.36, determine (a) a tração necessária no cabo se a resultante das três forças exercidas no ponto seja vertical, (b) a correspondente intensidade da resultante.
Passo 1
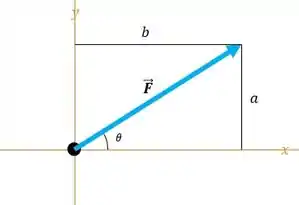
Bom galera, a gente vai encontrar as componentes horizontais e verticais de cada uma das forças que é dada por:
Passo 2
Show de bola, a gente sabe que a resultante será vertical, então a componente horizontal da resultante é , então vamos usar isso agora:
Passo 3
Por último, a gente calcular a soma das componentes na vertical, porque a resultante atuará apenas na vertical:
Resposta
Exercícios de Livros Relacionados
Uma força vertical de 1,8l b é aplicada ao botão do mecanismo de abertura de janela quando a manivela BC está na horizontal. Determine o momento da força sobre o ponto A e sobre a linha AB.
A matriz de rosqueamento é aparafusada na extremidade do tubo fixo, que é dobrado em um ângulo de 20 ° . Substitua as duas forças por uma força equivalente em O e um binário M O → . Encontre M O → e c
A força F → atua ao longo de um elemento do cone circular direito, como mostrado. Determine o sistema de força-binário equivalente no ponto O.
Duas forças atuam na placa retangular, conforme mostrado. Reduza este sistema de forças a um sistema de força-binário equivalente atuando no ponto O. Em seguida, determine a resultante do sistema, exp
No instante mostrado quando os crankpins de um motor de dois cilindros passam pelo plano horizontal y - z , a haste A está sob uma compressão de 1,8k N e a haste B está sob uma compressão de 0,8k N .