Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.9 - Ex. 175
175- Especifique o módulo e a localização da força resultante que atua em cada lado e no fundo do aquário, devido a água doce dentro dele.
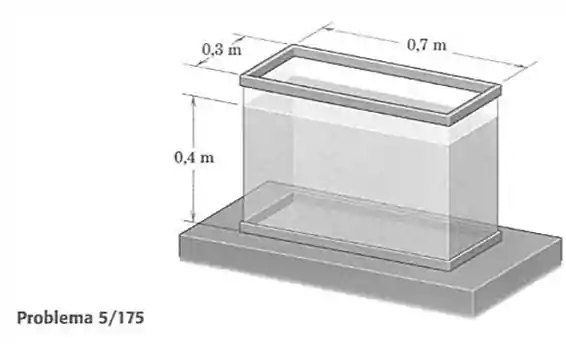
Passo 1
No fundo do aquário temos a influência do peso da água dentro da aquário que é dada por:
Onde a massa da água pode ser calculada por:
A densidade da água doce é dada por e o volume do aquário é:
Logo o peso da água será:
Passo 2
Agora calculando a força resultante no painel da frente, isso é onde tem as arestas de e .
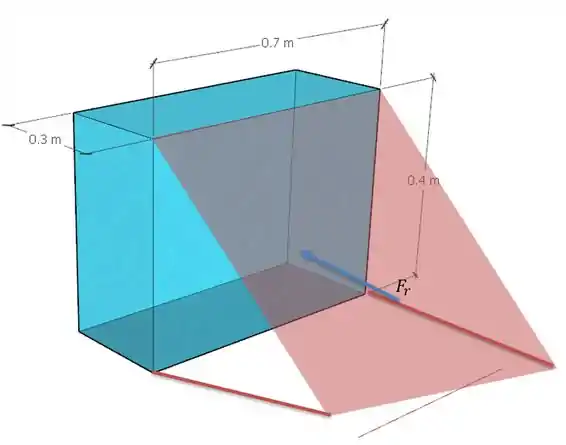
Para calcular a força resultante nesse lado do aquário temos que fazer a seguinte integral:
Passo 3
Agora para a área de arestas e e , o que nos dá a integral.
Todas as forças estão a de altura do aquário.
Resposta
Força no fundo do aquário:
Forças nos lados: e
Exercícios de Livros Relacionados
2.3. A força F = 900N atua sobre a estrutura. Decomponha essa força nas componentes que atuam ao longo dos membros AB e AC, e determine a intensidade de cada componente.
Determine a intensidade da força resultante e sua direção, medida no sentido anti-horário a partir do eixo x positivo.
2.7. Decomponha cada força que atua sobre o poste em suas componentes x e y
2.10. Se a força resultante que atua sobre o suporte for 750N direcionada ao longo do eixo x positivo, determine a intensidade de F e sua direção θ
2.12. Determine a intensidade da força resultante e sua direção θ, medida no sentido anti-horário a partir do eixo x.