Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 19.Problemas - Ex. 113

19.113. Um motor de massa M é suportado por molas com uma constante de mola equivalente k. O desbalanceamento de seu rotor é equivalente a uma massa m localizada a uma distância r do eixo de rotação. Mostre que quando a velocidade angular do rotor é f , a amplitude xm do movimento do motor é

x m = r m M ω f ω n 2 1 - ω f ω n 2

Onde ω n = k M

Passo 1

O melhor que fazemos para começar a questão é desenhar o problema.

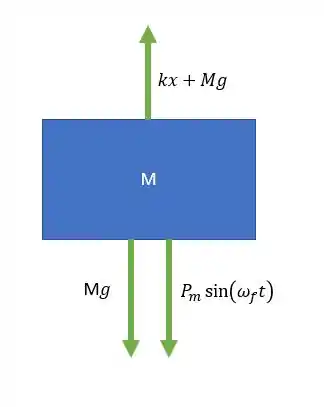
Aqui a gente tem que fixar atento com algumas coisas, por exemplo, a tensão na massa é variável

T = P m sin ⁡ ω f t

E as demais são a força da mola, e a força peso.

Bom, pela segunda lei de Newton temos:

∑ F = M y ¨

Então

M y ¨ = k x + M g - M g - P m sin ⁡ ω f t

Simplificando as coisas

M y ¨ = k x - P m sin ⁡ ω f t

A gente pode dividir tudo por M

y ¨ = k M x - P m M sin ⁡ ω f t

Isso é interessante para gente, porque podemos usar a equação do enunciado

ω n 2 = k M

E temos

y ¨ = ω n 2 x - P m M sin ⁡ ω f t

Passo 2

Agora vamos analisar o rotor:

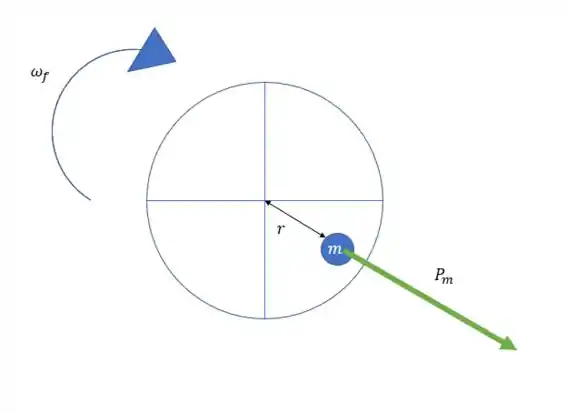
Repare que vai existir uma força centrifuga da pequena massa m quando o rotor gira, essa força é P m .

P m = m r ω f 2

Agora podemos usar a equação 19.33 do livro

x m = P m k 1 - ω f ω n 2

Mas é interessante para gente lembrar uma equação:

ω n 2 = k M

De novo esse resultado vai nos ajudar, pois com ele podemos concluir que

k = M ω n 2

Então

P m k = m r ω f 2 M ω n 2

Ou de forma mais organizada

P m k = r m M ω f 2 ω n 2

Passo 3

Então a equação de x m que estamos buscando fica

x m = P m k 1 - ω f ω n 2

x m = r m M ω f 2 ω n 2 1 - ω f ω n 2

Exatamente como queríamos demonstrar.

Resposta

x m = r m M ω f 2 ω n 2 1 - ω f ω n 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A engrenagem mostrada na figura tem raio R = 150 mm e raio de giração k - = 125 mm. A engrenagem está rolando sem deslizamento com velocidade v - 1 de intensidade 3 m/s quando ela bate em um degrau de
Um painel de madeira de 8 kg é suspenso por um pino suporte em A e está inicialmente em repouso. Uma esfera de metal de 2 kg é liberada do repouso em B e cai dentro de uma concha semiesférica C presa
Uma barra delgada uniforme AB de massa m está em repouso sobre uma superfície horizontal sem atrito quando o gancho C engata em um pequeno pino em A. Sabendo que o gancho é puxado para cima com uma ve
Uma barra delgada uniforme de comprimento L e massa m é apoiada por uma mesa horizontal sem atrito. Inicialmente, a barra está girando em torno de seu centro de massa G com uma velocidade angular cons
Um painel de madeira de 8 kg é suspenso por um pino suporte em A e está inicialmente em repouso. Uma esfera de metal de 2 kg é liberada do repouso em B’ e cai dentro de uma concha semiesférica C’ pres