Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 103
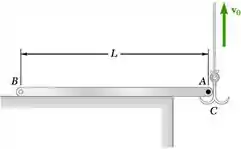
Uma barra delgada uniforme AB de massa m está em repouso sobre uma superfície horizontal sem atrito quando o gancho C engata em um pequeno pino em A. Sabendo que o gancho é puxado para cima com uma velocidade constante v0, determine o impulso exercido sobre a barra (a) em A, (b) em B. Considere que a velocidade do gancho fica inalterada e que o impacto é perfeitamente plástico.
Passo 1
O exercício pede que a gente determine o impulso exercido sobre a barra (a) em A, (b) em B. Considere que a velocidade do gancho fica inalterada e que o impacto é perfeitamente plástico.
Momento de inércia é dada por:
Cinemática. (Rotação sobre B)
Passo 2
Abaixo temos o esboço do momento para determinarmos .
Momentos sobre B.
Passo 3
Para isso realizamos 
Momentos sobre A.
-
Passo 2
- Para isso realizamos
Momentos sobre B
Resposta
Exercícios de Livros Relacionados
Em um jogo de sinuca, a bola A está rolando sem escorregar com uma velocidade Vo ao atingir obliquamente a bola B, que está em repouso. Denotando por r o raio de cada bola e por μ k o coeficiente de a
As barras uniformes AB e AC, cada uma com massa m e comprimento l, são parafusadas juntas em A e conectadas por pinos em pequenos roletes em B e C. Uma mola de constante k é presa aos pinos em B e C e
Uma bola de 20 g está ligada a uma raquete por meio de uma corda elástica AB de constante k = 7,5 N/m. Sabendo que a raquete é movida verticalmente de acordo com a relação δ = δ ms e nω ƒ t , ƒ com um
Para o disco do Problema, determine o intervalo de valores de ω ƒ ƒ para os quais a amplitude da vibração é menor que 3,5°.
Um motor de velocidade variável é rigidamente preso a uma viga BC.Quando a velocidade do motor é menor que 600 rpm ou mais que1.200 rpm, observa-se que um pequeno objeto em A permanece emcontato com a