Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 101

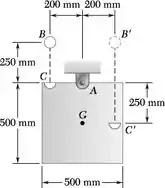
Um painel de madeira de 8 kg é suspenso por um pino suporte em A e está inicialmente em repouso. Uma esfera de metal de 2 kg é liberada do repouso em B’ e cai dentro de uma concha semiesférica C’ presa ao painel no mesmo nível do centro de massa G. Considerando que o impacto é perfeitamente elástico, determine a velocidade do centro de massa G do painel imediatamente após do impacto.

Passo 1

O enunciado pede que a gente determine a velocidade do centro de massa G do painel imediatamente após do impacto.

Massa e momento de inércia são dados a seguir :D

m S = 2   kg

m P = 8   kg

I - = 1 6 m P 0.5   m 2 = 1 6 8 0.5 2 = 0.3333   kg ∙ m 2

Passo 2

Velocidade da esfera em C.

v C 1 = 2 g y = 2 9.81   m/ s 2 0.25   m = 3.1321   m/s

Passo 3

Imediatamente após o impacto em termos de ω 2

A C ' = 0.2 2 + 0.25 2 = 0.32016   m

v C ' 2 = A C ' ω 2

= 0.32016 ω 2

v - 2 = 0.25   ω 2     θ               perpendicular a  A C

Passo 4

+ Momentos sobre C:

m S v C ' 1 0.2   m + 0 = m S v C ' 2 A C ' + I - ω 2 + m P v - 2 0.25   m

2   kg 3.1321   m/s 0.2   m = 2   kg 0.32016 ω 2 0.32016   m

+ 0.3333 ω 2 + 8   kg 0.25   m 2   ω 2

1.25284 = 0.2050 + 0.333 + 0.500 ω 2

ω 2 = 1.2066   rad/s

Passo 5

Velocidade do centro de massa:

v - 2 = 0.25   m ω 2 = 0.25   m 1.2066   rad/s = 0.3016   m/s

Resposta

v - 2 = 302   mm/s ←

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um disco uniforme de 8 kg e raio de 200 mm é soldado a um eixo vertical com uma ponta engastada em B. O disco gira em um ângulo de 3° quando um binário estático de intensidade de 50N ∙ m lhe é aplicad
A barra AB é rigidamente presa à estrutura de um motor em funcionamento com velocidade constante. Quando um cursor de massa m é colocado sobre a mola, observa-se que ele tem amplitude de 15 mm. Quando
As Figuras (1) e (2) mostram como molas podem ser usadas para suportar um bloco em duas situações diferentes. Na Fig. (1), elas ajudam a diminuir a amplitude da força oscilante transmitida pelo blocoà
Em um sistema com amortecimento subcrucial (c c c ), o período de vibração é usualmente definido como o intervalo de tempo τ d = 2π / ω d correspondente a dois pontos sucessivos onde a curva deslocame
Na prática, é frequentemente difícil determinar o decremento logarítmico de um sistema com o amortecimento subcrucial definido no Problema 19.129 pela medida de dois deslocamentos máximos sucessivos.