Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 102

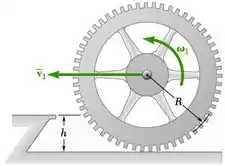
A engrenagem mostrada na figura tem raio R = 150 mm e raio de giração k - = 125 mm. A engrenagem está rolando sem deslizamento com velocidade v - 1 de intensidade 3 m/s quando ela bate em um degrau de altura h = 75 mm. Uma vez que a borda do degrau engata no dente da engrenagem, nenhum deslizamento ocorre entre a engrenagem e o degrau. Considerando um impacto perfeitamente plástico, determine a velocidade angular da engrenagem imediatamente após o impacto.

Passo 1

Pouco antes do impacto, o ponto de contato com a cremalheira é o centro instantâneo de rotação da engrenagem.

v - 1 = R ω 1 ←

Logo após o impacto, o Ponto S é o centro instantâneo de rotação.

v 2 = R ω 2     θ               perpendicular a  G S

Passo 2

+ Momentos sobre C:

m v - 2 R - h + I - ω 1 = m v - 2 R + I - ω 2

m R ω 1 R - h + m k - 2 ω 1 = m R ω 2 R + m k - 2 ω 2

R R - h + k - 2 ω 1 = R 2 + k - 2 ω 2

ω 2 = R 2 + k - 2 - R h R 2 + k 2 ω 1               ω 2 = 1 - R h R 2 + k 2 ω 1

Passo 3

Então temos os seguintes dados:

R = 150   mm ,               k - = 125   mm ,               v 1 = 3   m/s ,               h = 75   mm

ω 1 = v 1 R = 3   m/s 0.150   m = 20   rad/s

Velocidade angular.

ω 2 = 1 - 150 75 150 2 + 125 2 20   rad/s = 0.7049 20

Resposta

ω 2 = 14.10   rad/s  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O membro ABC tem uma massa de 2,4 kg e está preso a um suporte de pino em B. Uma esfera D de 800 g atinge a extremidade do membro ABC com uma velocidade vertical v1 de 3 m / s. Sabendo que L = 750 mm
Uma haste delgada CDE de comprimento L e massa em está ligada a um suporte de pino em seu ponto médio D. Uma segunda haste idêntica AB está girando em torno de um suporte de pino em A com uma velocida
Uma barra delgada uniforme AB de comprimento L = 800 mm é posicionada com seu centro equidistante de dois apoios localizados a uma distância b = 200 mm entre si. A extremidade B da barra é erguida a u
Resolva o problema 17.123, assumindo que o impacto entre as hastes é perfeitamente elástico.17.123 - Uma haste delgada AB é liberada do repouso na posição mostrada. Ela desce para a posição vertical e
A esfera A de massa m e raio r rola sem deslizar com uma velocidade V1 em uma superfície horizontal quando atinge uma esfera idêntica B que está em repouso. Denotando por u k o coeficiente de atrito c