Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.9 - Ex. 197
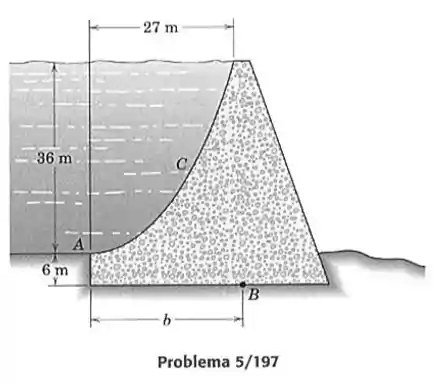
197- O lado cheio por água doce de uma represa de concreto tem a forma de uma parábola vertical com vértice em . Determine a posição do ponto na base da represa, pelo qual atua a força resultante da água contra a face da represa.
Passo 1
Primeiramente vamos apenas calcular a coordenada horizontal do centro de área da parte horizontal da água contida na região parabólica.
Toda parábola tem com equação característica uma forma como:
Porém como o vértice dessa função está em vamos considerar , logo vamos encontrar aplicando os pontos limites dessa parábola que seria e , logo:
Passo 2
A coordenada tem a seguinte equação para ser resolvida:
Onde o elemento de área é:
Preenchendo a região por linhas horizontais:
Porém:
Logo
Fazendo a integral dessa região no intervalo de 0 até :
Para fazer da forma tradicional basta descobrir o tamanho da linha horizontal e multiplicar pela altura . Isso é, fazer com que a função esteja em função de .
Por se tratar da linha horizontal logo o será igual a , logo:
Logo a coordenada horizontal do centro de área da parábola será:
Passo 3
No último passo conseguimos algumas informações valiosas, sabemos agora que a área da parte parabólica é de:
Com essa informação sabemos o peso dessa carga de água, considerando como sua densidade temos:
Já que não sabemos o volume, então multiplicamos a área por uma parcela de comprimento normal ao plano do papel:
O sistema de forças estará da seguinte maneira:
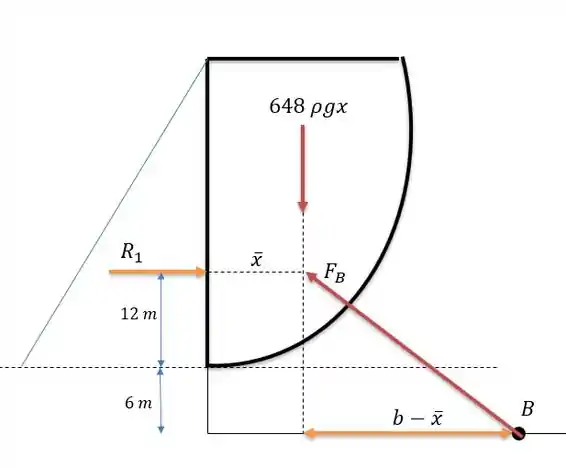
Onde representa a força de água na parte vertical e ela terá como valor:
Pois assim como não temos o volume para encontrar o peso da água na região parabólica nós também não temos a área transversal que essa área fará, somente a linha que vale e uma parcela de comprimento igual a de mesmo tamanho ao comprimento da represa. Logo valerá para densidade da água igual a :
Passo 4
Fazendo a somatória dos momentos em temos: