Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 20

20. A coluna retangular de madeira de 3 m tem as dimensões mostradas na figura. Determine a carga crítica, se considerarmos que as extremidades estão acopladas por pinos. E m = 12   G P a , σ e = 35   M P a .

Passo 1

Falaaa! Queremos achar a carga crítica para essa coluna. Vamos usar a fórmulinha:

P c r = π 2 E I ( K L ) 2

Como a base e o topo da coluna estão acoplado por pinos, já sabemos que o fator de comprimento efetivo K da nossa coluna é igual a 1 .

Temos também do enunciado que:

L = 3   m

E = 12   G P a   ( t a b e l a d o )

Só falta achar o momento de inércia I , né? Vamos partir para cima dele então!

Passo 2

Agora, vamos tratar de obter o momentos de inércia em relação ao eixo y do nosso sistema. Por que? Cara, esse eixo tem visualmente o menor momento de inércia. Então é em relação a ele que nossa coluna pode flambar.

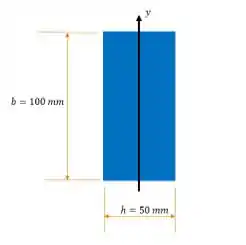
O momento de inércia vai ser:

I y = 0,1 0,05 3 12   m 4

Repara que para o eixo y , a base (segmento paralelo ao eixo) é 100   m m .

Pronto! Já sabemos o momento de inércia I y .

Passo 3

Vamos então, usar a expressão da carga crítica para a flambagem:

P c r = π 2 E I y ( K L ) 2

E substituindo os valores numéricos pertencentes a cada variável, chegamos até:

P c r = π 2 12 ⋅ 10 9   P a ( 1 ⋅ 3,0   m ) 2 ⋅ ( 0,100   m ) ( 0,050   m ) 3 12

P c r ≅ 13707,78   N ≅ 13,71   k N

Passo 4

Só falta a gente verificar se nossa carga é satisfatória, calculando o valor da tensão crítica também, né?! Porque essa carga não pode causar uma tensão que ultrapasse a tensão de escoamento do material, beleza?

Sabemos que ela é dada pela seguinte fórmula (a divisão da carga crítica pela área da seção transversal):

σ c r = P c r A

σ c r = P c r b h

σ c r = 13707,78   N ( 0,100   m ) ( 0,050   m )

σ c r ≅ 2,74   M P a

Esse valor é menor do que a tensão admissível para o nosso material, que é igual a 35   M P a . Logo, está tudo certo com o resultado!

Resposta

C a r g a   c r í t i c a → P c r ≅ 13707,78   N ≅ 13,71   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma coluna ideal com uma extremidade engastada e uma presa por pino. Mostre que a carga crítica é dada por P c r = 20,19 E I L 2 . .
A coluna ideal está sujeita à força F em seu ponto médio e à carga axial P. Determine o momento máximo da coluna no meio do vão.
A coluna está apoiada em B e esse apoio não permite rotação, mas sim deflexão vertical. Determine a carga crítica para EI constante.
Considere uma coluna ideal com ambas as extremidades engastadas. Mostre que a carga crítica é dada por P c r = 4 π 2 E I L 2 .
Considere que a coluna está em gastada na base e no topo. Determine a carga excêntrica máxima P que pode ser aplicada sem provocar flambagem ou escoamento da coluna. E m = 12 G P a e σ y = 56 M P a .