Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 79

79. Se F = 200   N , determine o ângulo θ necessário para que o momento de binário resultante seja zero.

Passo 1

Então o que o enunciado quer é achar um θ necessário para que o momento binário da foça 300   N , junto com o momento binário de F seja igual a 0   N ⋅ m .

Como o momento binário é um vetor livre (causa o mesmo efeito rotacional em qualquer ponto), vamos determinar ele em relação ao ponto central do disco.

Vamos calcular o momento binário usando a análise escalar:

M = F ⋅ d

Onde F é a intensidade das forças e d é a distância perpendicular ou braço de momento entre as forças.

Para resolver esse problema temos que deixar as forças F e - F perpendiculares em relação as seguintes linhas vermelhas:

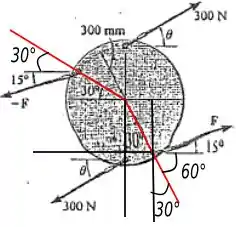
Para que assim seu braço de momento seja igual a 0,3   m .

Os ângulos encontrados na figura foram obtidos através de trigonometria. Então o ângulo que - F faz com a linha vermelha é 45 ° e que F faz com a linha vermelha é 75 ° .

Agora vamos achar as componentes perpendiculares.

Para - F :

- F ⋅ s e n   45 °

= - 200 ⋅ s e n   45 °

Para F :

F ⋅ s e n   75 °

= 200 ⋅ s e n   75 °

O momento binário resultante é a soma dos momentos binários das forças.

Vamos adotar o sentido horário como positivo.

As distâncias fornecidas na figura estão em m m , mas vamos passar para m .

Passo 2

Calculando:

0 = 300 ⋅ cos ⁡ θ 0,6 - 200 ⋅ s e n   75 ° 0,3 - 200 ⋅ s e n   45 ° 0,3

⇒ 0 = 180 ⋅ cos ⁡ θ - 57,95 - 42,4 2

⇒ 0 = 180 ⋅ cos ⁡ θ - 100,37

⇒ 100,37 = 180 ⋅ cos ⁡ θ

⇒ cos ⁡ θ = 0,557

⇒ θ = arccos ⁡ 0,557

⇒ θ = 56,1 °

Resposta

O ângulo necessário é:

θ = 56,1 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro de tração traseira está atolado na neve entre outros carros estacionados como mostrado. Em uma tentativa de livrar o carro, três estudantes exercem forças no casso nos pontos A , B e C , enqu
Sob condições não uniformes e escorregadias da estrada, as quatro forças mostradas são exercidas sobre as quatro rodas do veículo com tração nas quatro rodas. Determine a resultante desse sistema e as
Uma matriz está sendo usada para fazer uma rosca em uma barra. Se forças de 60N são aplicadas como mostrado, determine o módulo F das forças iguais exercidas na barra de 6m m de diâmetro por cada uma
Calcule o momento M O da força de 250N em relação ao ponto O na base do robô.
Reduza o sistema de carregamento dado a um sistema força-binário no ponto A . Em seguida, determine a distância x à direita do ponto A na qual atua a resultante das três forças.