Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 97
Sob condições não uniformes e escorregadias da estrada, as quatro forças mostradas são exercidas sobre as quatro rodas do veículo com tração nas quatro rodas. Determine a resultante desse sistema e as interseções e de suas linhas de ação. Observe que os eixos dianteiro e traseiro são iguais (ou seja, ).
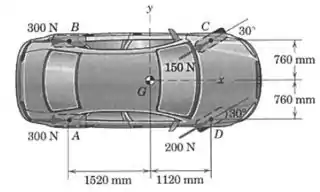
Passo 1
Vamos começar escrevendo as quatro forças em forma vetorial:
E agora podemos calcular a força resultante somando esses quatro vetores:
Passo 2
Agora precisamos calcular o momento total gerado por essas quatro forças, porque só assim saberemos onde deve ser aplicada. Lembrando que as forças que favorecem a rotação no sentido horário terão momento negativo.
As duas forças de tem mesmo módulo e direção, mas favorecem a rotação em sentidos contrários, então os seus módulos se anulam. Só precisamos considerar os momentos de cada componente das forças de e ( e ).
Começando por :
E agora :
Então o momento total é:
Passo 3
Agora queremos achar a linha de ação da força resultante. A força tem que ser aplicada em um ponto que mantenha o momento total das forças sobre o sistema.
Onde é o vetor do momento das forças em relação a e é o vetor posição do ponto onde a força será aplicada.
O vetor aponta na direção perpendicular ao plano do página, e (pela regra da mão direita) no sentido que sai desse plano.
Agora podemos resolver o produto vetorial:
E então:
Essa é a equação da linha de ação da força.
Passo 4
O enunciado pediu as interseções dessa linha de ação com cada um dos eixos e . Para calcular isso é só fazer algumas substituições:
Resposta
A força resultante é e os pontos de interseção da linha de ação são e .