Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 10.Problemas - Ex. 109

2014 - T 6 para a qual a tensão admissível à flexão é de 165,5 Mpa. Usando o método da interação, determine a menor dimensão d da seção transversal que pode ser usada quando e = 10,16   m m .

Passo 1

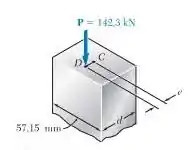
E ai gurizada o enunciado pede que a gente determine a menor dimensão d da seção transversal que pode ser usada quando e = 10,16   m m .

A = 2,25 d               c = 1 2 d               e = 0,4 i n .               L e = 36 i n .

σ a l l , b = 24   k s i           P = 32   k i p s

I x = 1 12 2,25 d 3       r x = d 12

Passo 2

Assume: r x = r m i n ,       i . e .           d < 2,25 i n .

L e r m i n = 12 L e / d

Assume L e r m i n > 55 .       σ a l l , c = 55,400 L e r x 2 = 55,400 d 2 12 L e 2 = 55,400 12 36 2 d 2 = 3,56224 d 2

P σ a l l , c + P e c I σ a l l , b = 32 2,25 d 3,56224 d 2 + 12 32 0,4 1 2 d 2,25 d 3 24 = 1

3,9925 d 3 + 1,42222 d 2 = 1         L e t   x = 1 d                   3,9925 x 3 + 1,42222 x 2 = 1

Passo 3

Resolvendo para x ,

x = 0,53126           d = 1 x = 1,8823 i n .   < 2,25   i n .

L r x = 12 36 1,894 = 65,8 > 55                                             d = 1,882 i n .

Resposta

1,882 i n .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tubo de alumínio com diâmetro externo de 3 in. suportará uma ação de 10 kips com uma excentricidade e = 0,6i n . Sabendo que o estoque de tubos disponíveis para uso é composto por elementos da liga
A haste rígida AB está presa a uma dobradiça em A e a duas molas, cada uma com k constante. Se h= 450 mm, d = 300 mm e 200 kg, m  determine a faixa de valores de k para a qual o equilíbrio da barra A
Determine (a) a carga crítica para a biela de aço, (b) a dimensão d para a qual a biela de alumínio terá a mesma carga crítica. (c) Expresse o peso da biela de alumínio como uma porcentagem do peso da
10.112: Resolva o Prob. 10.111 fazendo o projeto pelo método da interação com tensão de flexão admissível de 25 ksi.(10.111): Um tubo de alumínio com diâmetro externo de 3 in. suportará uma ação de 10
T 0 a força na coluna é zero e a flambagem ocorre quando a temperatura é T 1 = T 0 + Δ T ,e x p r e s s eΔ T em termos de b ,L e do coeficiente da expansão térmica α