Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 118
2/118)No projeto de um mecanismo de temporização , o movimento do pino A na ranhura circular fixa é controlado pela guia B , que está sendo elevado por seu parafuso de acionamento com uma velocidade constante para cima para um intervalo de seu movimento . Calcule ambas as componentes normal e tangencial da aceleração do pino A quando esse passa a posição em que .
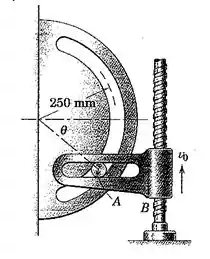
Passo 1
Então pessoal , para calcularmos as componentes normal e tangencial da aceleração do pino A , utilizaremos as relações já conhecidas :
Passo 2
Primeiramente, vamos achar uma relação entre a velocidade tangencial do pino e a sua velocidade na vertical.
Observe a figura abaixo e considere que a velocidade em vermelho é a velocidade na vertical, enquanto que a velocidade em cor preta é a velocidade tangencial:
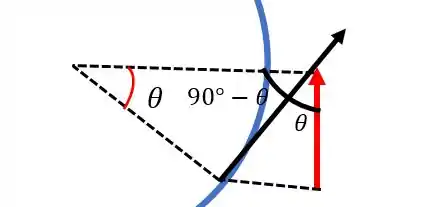
Podemos, então, achar a seguinte relação entre elas:
Ok? Bom, podemos achar também e :
Para achar é só derivar a equação acima:
O que fizemos ali em cima foi derivar em relação ao tempo, já que a única coisa que varia.
Assim, temos que:
Ok, agora podemos partir para resolver a questão.
Passo 3
Basta que apliquemos os valores agora: