Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 169

Um satélite da Terra movendo-se na órbita elíptica mostrada tem uma velocidade v = 17   970   k m / h quando passa pela extremidade do semieixo menor em A . A aceleração do satélite em A é devida à atração gravitacional e é 1,556   m / s 2 dirigida de A para O . Para a posição A calcule os valores de v ˙ e r ¨ .

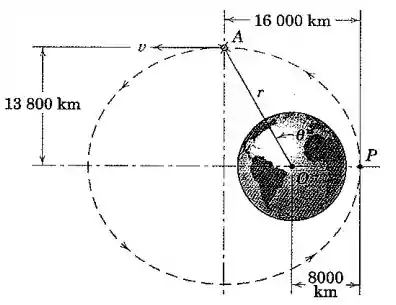
Passo 1

Galera, a velocidade v pode ser decomposta nas velocidades v r e v θ , como mostra a figura a seguir:

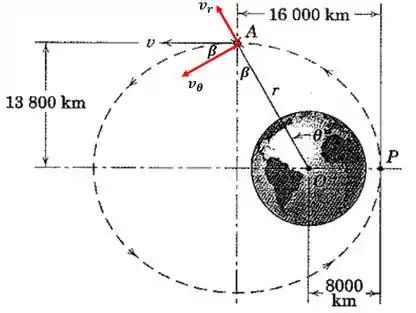
Note que a velocidade v θ faz um ângulo β com v . Note que esse é o mesmo ângulo presente no triângulo retângulo formado por A , O e o centro da elipse, portanto:

t g   β = 16000 - 8000   k m 13800   k m = 0,5797

β = t g - 1 0,5797

β = 30 °

Então, as componentes da velocidade são:

v r = v   s e n   β = 17970   s e n   30 ° = 8985   k m / h = 2496   m / s

v θ = v cos ⁡ β = 17970 cos ⁡ 30 ° = 15562   k m / h = 4323   m / s

Passo 2

Em coordenadas polares, temos:

v = r ˙   e r + r θ ˙   e θ

Ou seja, na direção de r , temos:

r ˙ = v r = 2496   m / s

E na direção perpendicular a esta:

r θ ˙ = v θ

θ ˙ = 4323   m / s r

Podemos calcular a distância r usando aquele triângulo retângulo:

cos ⁡ β = 13800   k m r

r = 13800   k m cos ⁡ 30 ° = 15935   k m = 15935 10 3   m

Então:

θ ˙ = 4323   m / s 15935 10 3   m

θ ˙ = 2,71 10 - 4   r a d / s

Passo 3

Agora, usamos a aceleração em coordenadas polares:

a = r ¨ - r θ ˙ 2   e r + r θ ¨ + 2 r ˙ θ ˙   e θ

O enunciado diz que a aceleração a = 1,556   m / s 2 se dirige de A para O , que é a mesma direção de e r , mas com sentido contrário, então:

r ¨ - r θ ˙ 2 = - 1,556   m / s 2

r ¨ - 15935 10 3 2,71 10 - 4 2 = - 1,556

r ¨ = - 0,3 9   m / s 2

Passo 4

Para descobrir v ˙ , temos que calcular a componente da aceleração a = 1,556   m / s 2 na direção de v , conforme mostra a figura:

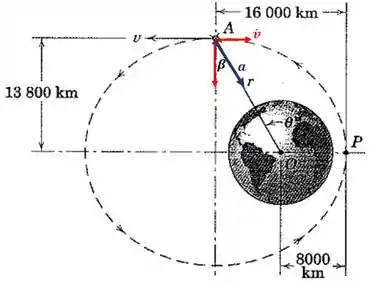
Então:

v ˙ = - a   s e n   β = - 1,556   s e n   30 °

v ˙ = - 0,778   m / s 2

Resposta

v ˙ = - 0,778   m / s 2

r ¨ = - 0,39   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma curva de transição em espiral é usada em ferrovias para ligar uma porção reta da linha férrea com uma porção curva. Se a espiral é definida pela equação y = 9 10 - 6 x 3 , onde x e y estão em metr
No instante θ = 30 ° , a came gira com uma velocidade angular no sentido horário de θ ˙ = 5r a d / s e aceleração angular de θ ¨ = 6r a d / s 2 . Determine as intensidades da velocidade e aceleração d
Se a came gira no sentido horário com uma velocidade angular constante de θ ˙ = 5r a d / s , determine as intensidades da velocidade e aceleração da barra seguidora A B no instante θ = 30 ° . A superf
O automóvel desce da garagem de um edifício por uma rampa em espiral a uma velocidade escalar constante de v = 1,5m / s . Se a rampa possui uma distância de 12m para cada volta descendente completa, θ
A caixa desce deslizando pela rampa helicoidal que é definida por r = 0,5m , θ = 0,5 t 3 r a d e z = 2 - 0,2 t 2m , onde t é dado em segundos. Determine as intensidades da velocidade e aceleração da c