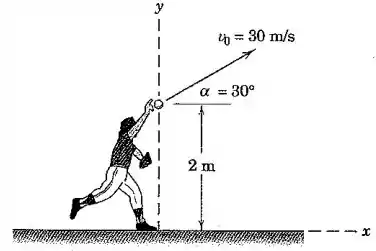
O jogador de beisebol do Prob. 2/126 é repetido aqui com o fornecimento de informações adicionais. No instante t = 0 , a bola é arremessada com uma velocidade inicial de 30m / s em um ângulo de 30 ° em relação à horizontal. Determine as grandezas r , r ˙ , r ¨ , θ , θ ˙ e θ ¨ , todas em relação ao sistema de coordenadas x - y mostrado, no instante t = 0,5s .

r = 15,40m r ˙ = 27,3m / s r ¨ = - 3,4m / s 2 θ = 32,5 ° θ ˙ = - 0,35r a d / s θ ¨ = 0,7r a d / s 2

Enunciado

Primeiro, vamos calcular as componentes em e da aceleração, velocidade e posição da bola quando . Em , temos movimento uniforme, então:

Já em , temos movimento uniformemente variado:

Observe a figura:

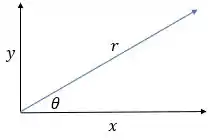
Assim, calculamos a distância da bola à origem:

E o ângulo com a horizontal é obtido:

Analogamente, calculamos o módulo da velocidade total e o ângulo que essa velocidade faz com a horizontal:

Agora escrevemos a velocidade em coordenadas polares:

Pra gente conseguir decompor a velocidade em termos dessas coordenadas, observe a figura:

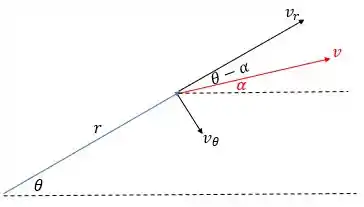
Então, na direção de , temos:

A velocidade está no sentido oposto ao de , portanto:

Como a aceleração horizontal é nula, temos:

Decompomos a aceleração assim:

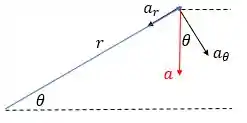
Em coordenadas polares, a expressão da aceleração é desse jeito:

A aceleração está no sentido oposto ao de , então:

A aceleração está no sentido oposto ao de , portanto: