Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 120

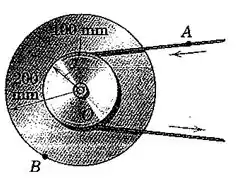
2/120) A roda e a polia acoplada giram sobre o eixo fixo em O e são acionadas pela correia mostrada . Em um determinado instante a velocidade e a aceleração de um ponto A sobre a correia são 0,6 m / s e 2 m / s 2 , respectivamente , os dois na direção mostrada . Calcule o móduloda aceleração total do ponto B sobre a roda para esse instante . Observe que o movimento linear do ponto A sobre a correia e o movimento tangencial de um ponto sobre o círculo de raio 100   m m são idênticos e que θ ' e θ " para as linhas radiais para todos os pontos sobre a roda são iguais .

Passo 1

Então pessoal , para resolvermos essa questão basta aplicarmos as fórmulas que já conhecemos. Sabemos que :

v = r θ '

Dessa forma :

v B = 8 4 2 = 4   f t / s

Agora que temos a velocidade em B , podemos calcular a aceleração normal através da relação :

a n = v 2 r  

  a n = 4 2 8 12 = 24   f t / s 2

Passo 2

Além disso nós sabemos que a aceleração tangencial é dada por :

a t = r θ "  

Sendo assim , temos que :

a t = 8 4 . 6 = 12 f t s 2    

Agora podemos achar a aceleração total em B através da fórmula :

a B = 24 2 + 12 2 = 26,8   f t / s 2

Resposta

a B = 26,8   f t / s 2

Suave pessoal? Então partiu fazer mais exercícios como esse!!!!!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a velocidade escalar constante máxima que um carro de corrida pode ter se a aceleração do carro não pode exceder 7,5m / s 2 enquanto gira em uma pista tendo um raio de curvatura de 200m .
Um carro viaja ao longo de uma pista circular de raio 75m , e sua velocidade escalar por curto período de tempo 0 ≤ t ≤ 2s e v = 0,9 t + t 2m / s , onde t é dado em segundos. Determine a intensidade d
O barco move-se ao longo de uma linha reta com a velocidade escalar descrita pelo gráfico. Construa os gráficos s - t e a - s . Determine também o tempo necessário para o barco se deslocar a distancia
O anel de 2,5 kg desliza sobre a barra lisa, de maneira que quando ele está em A ele tem velocidade de 3 m/s. Se a mola à qual ele está ligado tem comprimento não deformado de 0,9 m e rigidez de k = 1
Uma partícula de 2 kg desloca-se ao longo de uma trajetória lisa horizontal definida por r = 1 4 t 3 + 2m , θ = t 2 4r a d Onde t é dado em segundos. Determine as componentes da força radial e transve