Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.11 - Ex. 103

103. O rotor de 210   k g do motor de um avião turbojato tem um raio de giração de 220   m m e gira no sentido anti-horário a 18000   r p m quando visto de frente. Se o avião está viajando a 1200   k m / h e começa a executar uma acrobacia aérea na forma de um círculo em um plano vertical de 3800   m de raio, calcule o momento giroscópico M transmitido à estrutura do avião. Que correção nos controles o piloto deve fazer a fim de permanecer no plano vertical?

Passo 1

Primeiro, vamos montar o diagrama de corpo livre do rotor:

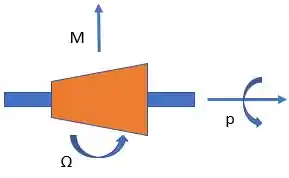
Assim, podemos verificar como fica aplicado o momento M no avião, visto de cima:

Aqui, podemos analisar que o piloto deve virar o leme para a esquerda a fim de compensar o momento giroscópico.

Passo 2

Agora, vamos calcular o valor de M . Para isso, precisaremos da fórmula:

M = I Ω ⋅ p

Dando início aos nossos cálculos, bora determinar primeiro o momento de inércia. Sabemos que o raio de giração é dado pela fórmula:

k = I m

I = m k 2

I = 210   k g ⋅ ( 0,220   m ) 2

I = 10,164   k g ⋅ m 2

O nosso Ω ali é a precessão da roda, que é calculada por:

Ω = v r

Ω = 1200 × 10 3   m 3600   s ⋅ 1 3800   m

Ω = 0,0877   s - 1

E para p temos que achar a velocidade angular. Como ela foi dada em r p m , devemos transformá-la em r a d / s pela fórmula:

ω = 2 π f

Onde f é a frequência. Assim, devemos dividir o valor dado por 60 para mudar de minutos para segundo:

ω = 2 π ⋅ 1800   r p m 60

ω ≅ 188,495   r a d / s

Finalmente, encontrado todos os valores que precisamos; bora logo tratar de achar o momento M :

M = ( 10,164   k g ⋅ m 2 ) ( 0,0877   s - 1 ) ( 188,495   r a d / s )

M ≅ 1681   N ⋅ m

Resposta

O piloto deve virar os controles para a esquerda para permanecer no plano vertical e o momento giroscópico M transmitido à estrutura do avião é de ( M ≅ 1681   N ⋅ m )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cone circular reto é formado girando-se a área sombreada em torno do eixo x . Determine o momento de inércia I x e expresse o resultado em termos da massa total m do cone. O cone tem uma densidade c
O tronco de cone é formado girando-se a área sombreada em torno do eixo x . Determine o momento de inércia I x e expresse o resultado em termos da massa total m do tronco. O tronco tem uma densidade c
O paraboloide é formado girando-se a área sombreada em torno do eixo x . Determine o momento de inércia em relação ao eixo x e expresse o resultado em termos da massa total m do paraboloide. O materia
O paraboloide é formado girando-se a área sombreada em torno do eixo x . Determine o raio de giração k x . A densidade do material é ρ = 5 Mg/m3.
Determine o momento de inércia I y do sólido formado girando-se a área sombreada em torno do eixo y . A densidade do mateirla é ρ . Expresse o resultado em termos da massa m do semielipsoide.