Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.9 - Ex. 228

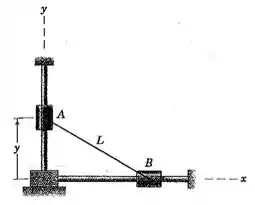
2/1228) Os anéis e deslizam ao longo das hastes fizas em ângulo reto e estão conectados por um fio de comprimento . Determine a aceleração do anel em função de se o anel possui uma velocidade constante para cima .

Passo 1

Então galera , seja a distância do anel ao pé da haste fixa , a distância do anel ao pé da haste fixa e o comprimento do fio que liga os anéis . Aplicando Pitágoras , temos que :

Agora derivamos a equação acima paraobtermos a relação entre as velocidades :

Reparem que como é uma constante , a sua derivada é zero!

Passo 2

Usando raciocínio análogo ao do item anterior , derivamos pela segunda vez para obtermos a relação entre as acelerações :

Como , temos que a sua derivada .

Dessa forma , isolando na equação achada anteriormente , obtemos que :

Como , temos que:

Resposta

Suave galera? Então bora resolver mais questões como essa!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2/223)Sob aação da força P , aaceleração constante do bloco B é de 2 m / s 2 para cima do plano inclinado . Para o instante em que a velocidade de B é de 1,2m / s subindo o plano inclinado , determine

2/227) A fim de acelerar a elevação dos fardos representados no exemplo 2/16 , o arranjo das polias é alterado como mostrado aqui . Se o trator A tem uma velocidade para a frente v A , determine uma e

2/226) O andaime do Prob.2/225 é modificado aqui pela colocação dos guinhos motorizados no chão em vezde no andaime . As outras condições permanecem as mesmas . Calcule a velocidade de subida v do and

Sob ação da força P , a aceleração constante do bloco B é de 3m / s ² ² para a direita. No instante em que a velocidade de B é de 2m / s para a direita, determine a velocidade de B em relação a A , a