Se o caminhão do Prob. 3/19 faz uma parada a partir de uma velocidade inicial de em uma distância de com desaceleração uniforme, determine se o caixote bate ou não na proteção na extremidade dianteira da carroceria. Se o caixote bate na proteção, calcule sua velocidade em relação ao caminhão quando o impacto ocorre. Utilize os coeficientes de atrito e .
Prob. 3/19: O coeficiente de atrito estático entre a superfície plana da carroceria do caminhão e o caixote que este carrega é . Determine a distância mínima de parada que o caminhão pode ter a partir de uma velocidade de com desaceleração constante se o caixote não deve deslizar para frente.
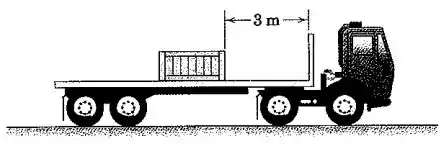
Passo 1
Conforme calculamos no Prob. 3/19, a distância mínima de parada do caminhão para que o caixote não deslizasse seria de . Mas no caso do nosso problema agora, temos , ou seja, com certeza o caixote vai deslizar.
Então, atuará sobre o caixote uma força de atrito dinâmico , cujo módulo será:
Aplicando a Segunda Lei de Newton ao caixote, obtemos a aceleração do caixote:
Passo 2
Para calcular a aceleração do caminhão, usamos a seguinte equação do movimento uniformemente acelerado:
Aqui temos e , quando :
Desse modo, a aceleração relativa do caixote em relação ao caminhão será:
Então, a velocidade de batida do caixote na carroceria do caminhão (se realmente acontecer) em relação ao caminhão, quando , pode ser dada por:
Passo 3
Para verificar que a batida realmente acontece antes do caminhão parar, vamos calcular o tempo até a batida, usando a seguinte equação do movimento uniformemente acelerado:
Nesse tempo , vamos calcular qual distância o caminhão andou:
Ou seja, como no instante de batida calculado, a batida realmente acontece.
Resposta
A batida acontece com velocidade relativa de .