Sob ação da força , a aceleração constante do bloco é de para a direita. No instante em que a velocidade de é de para a direita, determine a velocidade de em relação a , a aceleração de em relação a , e a velocidade absoluta do ponto do cabo.
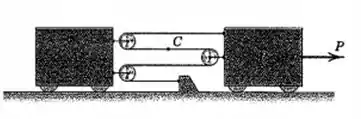
Passo 1
O bloco é o da direita, e o bloco é o da esquerda. É essencial ter uma mentalidade mais “geométrica” para resolver esses problemas, não fique muito apegado à física, porque essas situações não são fáceis de imaginar.
Em geral, para resolver esses problemas, você deve associar a velocidade de alguém com algum valor geométrico!
Vamos começar definindo um referencial de deslocamento: o zero vai estar à esquerda do bloco :
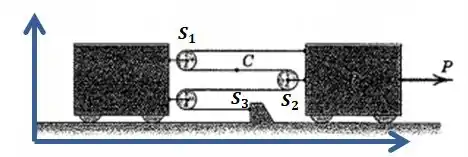
Usando esse referencial a gente pode dar nomes às posições das roldanas, ao ponto e ao encaixe no chão.
Passo 2
Olhe bem para a figura, vamos escrever uma expressão para o comprimento da corda:
Ok. A roldana está presa ao bloco , e a roldana está presa ao bloco , ou seja: as derivadas temporais dessas posições são as velocidades de e .
E o ponto está preso ao chão, então sua derivada é nula, porque ela é constante no tempo, assim como o comprimento da corda.
Então derivando a fórmula do comprimento:
Beleza, temos nosso primeiro resultado importante.
Passo 3
Agora podemos derivar essa expressão mais uma vez, para encontrar uma relação entre as acelerações dos blocos:
Ok, então temos:
E o primeiro objetivo é: determinar a velocidade de em relação a quando .
Então a velocidade de em relação a é:
Passo 4
O segundo objetivo é: sabendo que a aceleração do bloco é constante e igual a , qual a aceleração do bloco em relação a . Vamos fazer a mesma coisa de antes:
E então a aceleração relativa é:
Passo 5
Agora falta descobrir a velocidade absoluto do ponto do cabo.
Vamos escrever uma expressão para o comprimento do cabo entre o ponto e a extremidade do cabo que está presa ao bloco .
Aqui estamos desconsiderando aquele “pedacinho” de cabo entre a roldana e o bloco, o que não vai fazer diferença no final das contas, já que vamos derivar essa expressão.
E usando as velocidades que nós calculamos lá em cima:
Agora sim, resolvido!
Resposta
A velocidade de em relação a é e a aceleração é . A velocidade absoluta do ponto é .