Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.9 - Ex. 227

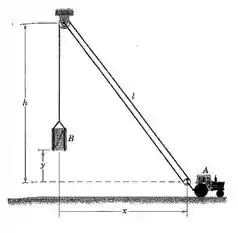
2/227) A fim de acelerar a elevação dos fardos representados no exemplo 2/16 , o arranjo das polias é alterado como mostrado aqui . Se o trator A tem uma velocidade para a frente v A , determine uma expressão para a velocidade de subida v B do fardo em termos de x . Despreze a pequena distância entre o trator e sua polia de modo que ambos têm essencialmente o mesmo movimento . Compare seus resultados com os do exemplo 2/16 .

Passo 1

Então galera, para resolvermos exercícios desse tipo , devemos primeiramente calcular o comprimento do cabo que aparece na imagem . E para isso , definimos que :

h   é a distância vertical entre os centros das duas polias .

y   é a distância do centro da polia menos elevada até o bloco B .

x é a distância horizontal entre os centros das duas polias .

Com essas propriedades definidas , temos que o comprimento do cabo é dado por :

L = h - y + 2 l + c o n s t a n t e = h - y + 2 x 2 + h 2 + c o n s t a n t e

Passo 2

Derivando a equação do comprimento do cabo para obtermos a relação com as velocidades , achamos que :

L ' = 0 = - y ' + 2 x x ' x 2 + h 2

Substituindo v A por x ' e v B por y ' , obtemos que :

v B = 2 x x 2 + h 2 v A

Resposta

v B = 2 x x 2 + h 2 v A

E aí , topa fazer mais exercícios com a gente?

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2/118) Para o sistema de polias mostrado , cada um dos cabos em A e B recebe uma velocidade de 2 m / s na direção da seta . Determine a velocidade ascendente v da carga m .
Um caminhão equipado com um guincho motorizado sobre a sua dianteira puxa a si próprio para cima num aclive íngreme com o arranjo de cabo e polia mostrado. Se o cabo é enrolado sobre o tambor na taxa
Em um dado instante, o cilindro A tem uma velocidade para baixo de 0,8m / s e uma aceleração para cima de 2m / s 2 . Determine a velocidade e a aceleração correspondentes do cilindro B .
Determine a equação de restrição que relaciona as acelerações dos corpos A e B . Assuma que a superfície superior de A permanece na horizontal.
Se o bloco A tem uma velocidade de 0,6m / s para a direita, determine a velocidade do cilindro B .