Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 14
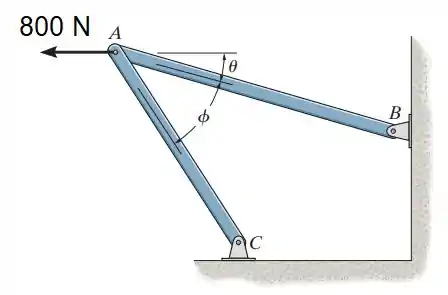
2.14. Determine o ângulo para o tirante AB, de modo que a força horizontal de tenha uma componente de direcionado de A até C. Qual é a componente da força que atua ao longo do membro AB? Considere
Passo 1
Vamos analisar os vetores
Se a gente rearrumar os vetores formamos a imagem
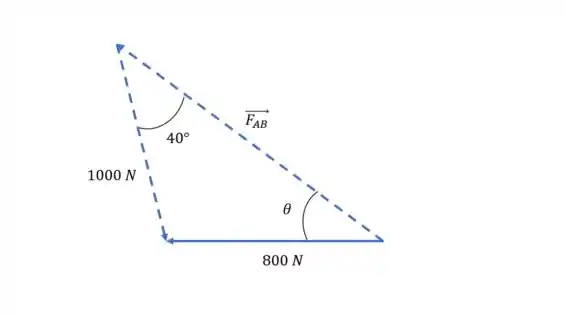
Daqui podemos extrais o seguinte triângulo
Passo 2
Podemos descobrir θ usando a lei dos senos
Agora, usando a propriedade que diz que a soma dos ângulos internos de um triângulo é 180°, podemos determinar o último ângulo que falta, vamos chamar ele de
Passo 3
Agora podemos usar novamente a lei dos senos para determinar a força
Resposta
Exercícios de Livros Relacionados
Demonstre que ∇ ln r = r r 2
X é um vetor desconhecido que satisfaz as relações a seguir envolvendo os vetores conhecidos A e B e a grandeza escalar φ , A × X = BeA ∙ X = φ Expresse X em termos de A, B, φ e a magnitude de A.
Uma partícula se move em uma órbita elíptica plana descrita pelo vetor de posição r = 2 b s e nω t i + b c o sω t j a )D e t e r m i n ev ,aeav e l o c i d a d ed ap a r t í c u l a . í b )Q u a léoâ
Obtenha a lei do cosseno da trigonometria plana interpretando o produto (A - B) . (A - B) e a expansão do produto.
Considere a, b, c como sendo três vetores constantes traçados a partir da origem até os pontos A, B e C. Qual é a distância da origem até o plano definido pelos pontos A, B, C? Qual é a área do triâng