Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 143
2.143 Os três cabos de suporte exercem as forças mostradas na figura. Represente cada força como um vetor unitário.
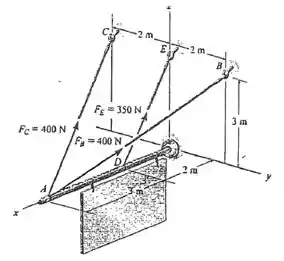
Passo 1
Nós temos o módulo das forças, mas precismos representar elas como um vetor. Para isso vamos achar o vetor com módulo 1 que está na mesma direção e sentido de cada uma das forças e então multiplica-las pelos vetores de módulo 1.
Vamos começar com o vetor para a força .
Nós podemos pegar o vetor que vá de A até B, , pois temos suas coordenadas, e dividi-lo pelo seu módulo, dessa forma seu tamanho será reduzido a um, mas sua direção e sentido vão continuar as mesmas.
Seu módulo é igual a
Vou chamar de o vetor de módulo 1, que ira dar a direção e o sentido da força :
Passo 2
Para achar a força em vetor unitário só precisamos multiplicar seu módulo pelo vetor :
Passo 3
Para os vetores e , devemos fazer a mesma coisa que fizemos anteriormente.
Vamos achar o vetor :
Agora o vetor de módulo 1:
Agora é só multiplicar esse vetor pelo módulo da força
Passo 4
Só falta acharmos , para isso vamos calcular e seu módulo
Agora o vetor de módulo 1:
Mais uma vez, agora só falta multiplicar o vetor pelo módulo da força: