Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 171
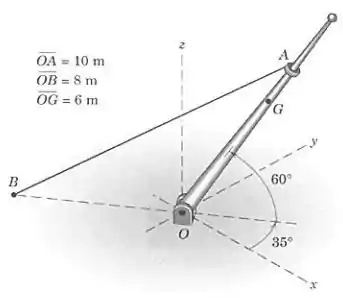
Quando o mastro está na posição mostrada, a força trativa no cabo vale .
(a) Usando as coordenadas mostradas, escreva na forma vetorial a força trativa exercida na pequena arruela no ponto .
(b) Determine o momento dessa força em relação ao ponto e indique os momentos em relação aos eixos , e .
(c) Determine a projeção desta força trativa sobre a linha .
Passo 1
(a) Olhe o seguinte desenho:
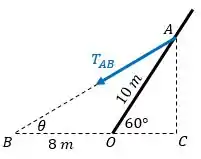
Podemos calcular a medida por meio da lei dos cossenos:
Então, a força trativa na forma vetorial será:
Passo 2
(b) Calculamos o momento em relação ao ponto assim:
E então:
Passo 3
(c) O módulo da projeção da força sobre a linha é obtido por meio do produto escalar:
onde é o vetor unitário nessa direção.
Então:
Resposta
(a)
(b)
(c)
Exercícios de Livros Relacionados
Se F a = 7 k NeF b = 5 k N , substitua o sistema de forças que age sobre as mísulas por uma força resultante e especifique sua posição sobre o plano x - y .
Determine as intensidades de F aeF b de modo que a força resultante passe pelo ponto O da coluna.
Substitua as três forças atuando na chapa por um torsor. Especifique a intensidade da força e o momento de binário para o torsor e o ponto P ( x , y ) onde sua linha de ação intercepta a chapa.
Se F a = 40 k N e F b = 35 k N , determine a intensidade da força resultante e especifique a posição de seu ponto de aplicação ( x , y ) sobre a placa.
Substitua as três forças que agem na chapa por um torsor. Especifique a intensidade da força e o momento de binário para o torsor e o ponto P ( x , y ) , onde sua linha de ação intercepta a chapa.