Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 173

Três binários são formados por três pares de forças iguais e opostas. Determine a resultante M dos três binários.

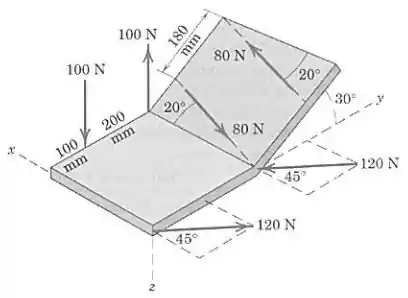
Passo 1

Olhando apenas para o binário de forças de 100   N , o momento combinado M 100 será:

M 100 = - 100   0,200   i

M 100 = - 20   i   N ∙ m

Fazemos o mesmo com o binário de forças de 80   N :

M 80 = 80   0,180 cos ⁡ 20 ° - j   s e n   30 ° - k cos ⁡ 30 °

M 80 = - 6 , 7 66   j - 11,7 19   k   N ∙ m

Passo 2

Por último, calculamos o binário de 120   N :

M 120 = - 120   0,300 cos ⁡ 45 °   k

M 120 = - 25,456   k   N ∙ m

Então, só resta somar os três binários para obter a resultante M :

M = M 100 + M 80 + M 120

M = - 20   i + - 6,766   j - 11,719   k + - 25,456   k

M = - 20   i - 6,77   j - 37,2   k   N ∙ m

Resposta

M = - 20   i - 6,77   j - 37,2   k   N ∙ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A força horizontal de 30N atua no cabo da chave. Qual é a intensidade do momento dessa força em relação ao eixo z ?
A força horizontal de 30N atua no cabo da chave. Determine o momento dessa força em relação ao ponto O . Especifique os ângulos de direção coordenados α , β e γ do eixo do momentos.
Determine a componente projetada da força F a b = 560 N que atua ao longo do tubo A C . Expresse o resultado como um vetor cartesiano.
Substitua o sistema de forças paralelas que age sobre a chapa por uma força resultante equivalente e especifique sua posição no plano x - z .
Substitua o sistema de forças e momentos binário que agem sobre o bloco retangular por um torsor. Especifique a intensidade da força e o momento de binário do torsor e a posição onde sua linha de ação