Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 172
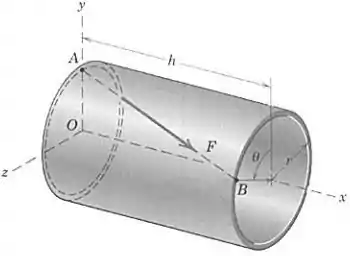
Uma força atua ao longo da linha dentro da casca cilíndrica circular, como mostrado. As quantidades , , e são conhecidas. Usando as coordenadas , e mostradas, expresse como um vetor.
Passo 1
Note que as coordenadas do ponto são:
E as coordenadas do ponto são:
Logo, o vetor que vai de para será:
Passo 2
Agora, lembre-se de que podemos escrever desse modo:
onde é o vetor unitário na direção e sentido de , que vai de para . Esse vetor pode ser obtido a partir do vetor posição , olha só:
Resposta
Exercícios de Livros Relacionados
Se a força resultante deve agir no centro da placa, determine a intensidade das cargas das colunas F aeF b e a intensidade da força resultante.
Se a força em cada corrente possui uma intensidade de 2,25 k N , determine a intensidade e os ângulos de direção coordenados da força resultante.
Se a resultante das três forças é F r = - 4,5 kk N , determine a intensidade da força em cada corrente.
As forças e binários mostrados na figura são aplicados em dois parafusos à medida que uma chapa metálica é parafusada em um bloco de madeira. Reduza as forças e os binários a um torsor equivalente e d
Dois parafusos A e B são apertados aplicando-se as forças e os binários mostrados na figura. Substitua os dois torsores por um torsor único equivalente e determine a a resultante R , b o passo do tors