Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 148
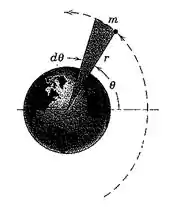
2/148) Um satélite se desloca em uma órbita elíptica em volta da terra . Não há nenhuma força sobre o satélite na direção , de modo que . Prove que a segunda lei de Kepler do movimento planetário que afirma que a linha radial varre área iguais em intervalos de tempo iguais . A área varrida pela linha radial durante o intervalo de tempo é sombreada na figura .
Passo 1
Então galera , nós sabemos que é dado por :
Além disso , temos que :
Isso se deve ao fato de que :
Como a aceleração angular é nula , a velocidade angular é costante . Sendo assim a linha radial varre área iguais em intervalos de tempo iguais .
Resposta
De boa galera? Então vamos para a próxima!
Exercícios de Livros Relacionados
2/118)No projeto de um mecanismo de temporização , o movimento do pino A na ranhura circular fixa é controlado pela guia B , que está sendo elevado por seu parafuso de acionamento com uma velocidade c
2/121) O projeto preliminar de uma “pequena”estação espacial para orbitar a terra em uma trajetória circular consiste em um anel (toro) com uma seção transversal circular como mostrado . O espaço habi
2/120) A roda e a polia acoplada giram sobre o eixo fixo em O e são acionadas pela correia mostrada . Em um determinado instante a velocidade e a aceleração de um ponto A sobre a correia são 0,6 m / s
2/117) Para simular uma condição de “ausência de peso”na sua cabine , um avião de transporte a jato viajando a 800 k m / h se desloca continuamente em umacurva vertical como mostrado . A que taxa β '
2/124) Uma pequena partícula P parte do ponto O com uma velocidade desprezível e aumenta sua velocidade para umvalor v = 2 g y , onde y é a altura vertical a partir de O . Quando x = 15m , determine a