Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 163
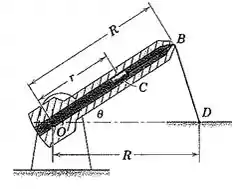
2/163) O braço com rasgo é articulado em e sustenta o cursor . Aposição de no rasgo é determinada pelo cordão que está preso em e permanece esticado . O braço gira no sentido anti-horário com uma velocidade angular constante durante um intervalo de seu movimento . O comprimento do cordão é igual a , o que faz quando . Determine o módulo da aceleração do cursor na posição para o qual . A distância é de .
Passo 1
Então galera , analisando o enunciado e a figura do problema , obtemos que :
Sendo assim , para :
Passo 2
Com os dados achados anteriormente , podemos facilmente achar as componentes através das relações :
O módulo da aceleração , por sua vez , é dado por :
Resposta
Suave pessoal? Então partiu fazer mais exercícios como esse!!!!!
Exercícios de Livros Relacionados
2/122) O projeto de um sistema de comando de válvulas de um motor de autonóvel de quatro cilindors é mostrado. Quando o motor é acelerado , a velocidade da correia v varia uniformemente de 3 m / s até
2/119) Um foguete viajando acima da atmosfera a uma altitude de 500k m teria uma aceleração em queda livre g = 8,43 m / s 2 na ausência de outras forças que não a atração gravitacional . Devido ao emp
2/123) Adireção do movimento de uma fita plana em um dispositivo de controle numérico é alterada pelas duas polias A e B mostradas . Se a velocidade da fita aumenta uniformemente a partir de 2 m / s a
2/125) Uma fita magnética corre sobre a polia louca em um computador conforme mostrado . Se aceleração total de um ponto P sobre a fita em contato com a polia faz um ângulo de 4 ° com a tangente á fit
2/127) Para a bola de beisebol do Prob. 2/126 , determine o raio de curvatura ρ da trajetória e a taxa de variação no tempo v ' da nos instantes t = 1s e t = 2,5s onde t = 0 é o instante do lançamento